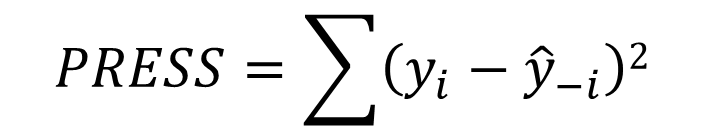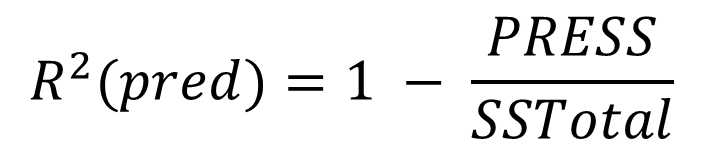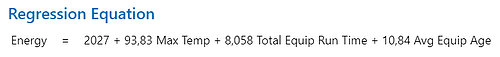控制图教程和示例
无论您是刚开始使用控制图,还是精通统计过程控制,都会在我们的控制图相关的文章中找到一些有价值的信息和引人深思的内容。
不同类型的控制图
您在统计学中最先学到的内容之一是,当涉及到数据时,没有一种方法能够放之四海皆准。为了从分析中获得最有用和最可靠的信息,需要选择最适合您的数据类型的方法类型。
对于控制图也是如此。尽管有一些控制图的使用频率极高,但是可供使用的控制图有许多,选择正确的控制图能够对可行性信息和误报(或漏报)进行区分。
《我应当使用哪个控制图?》 简要概述了最常见的控制图,并探讨了如何使用“协助”来帮助您选择适合您的情况的控制图。如果您是控制图新手,并且想了解有关我们为何使用控制图的更多背景,请查看《控制图显示重要的变异》。
我们在《超越“普通”控制图:EWMA 控制图》中赞颂了一个不太常用的控制图。
在 《Minitab 软件开发中使用 Laney P' 控制图》中,Dawn Keller 探讨了 P' 控制图及其变体之间的区别,Tammy Serensits 在《P 和 U 控制图和林堡干酪:一种糟糕的组合》中对此进行了描述。
一定要记住事情并不总是看起来那么复杂,有时候简单的解决方案和更复杂的方法一样有效。查看《放轻松:创建运行图》了解原委。
控制图教程
我们的许多 Minitab 博主都谈到了在特定条件下选择、创建和解释控制图的过程。如果您的数据无法在子组中收集,您可能需要了解《如何创建和读取 I-MR 控制图》。
如果您的数据可以在子组中收集,则在谈到《控制图:子组大小很重要》时,您将需要了解具体原因。
通常,有用的做法是以基于日历的增量查看控制图数据,在《创建控制图以比较月度变化》和创建控制图以比较月度变化(第 2 部分)》系列博客中探讨了每月方法。
如果您想了解您的过程改进所带来的差异,请查看《改进前后的过程分析:具有阶段的历史控制图》和《设置阶段:在控制图中说明过程变更》。
尽管控制图的基本理念非常简单,但解释真实世界的控制图可能有点棘手。请务必阅读 《 Minitab 中的控制图稳定性报告包括示例模式》帖子,了解“协助”中的一个重要功能。
最后,我们的一位专家级统计培训师为您建议了《五种使控制图更有效的方法》。
控制图示例
控制图最常用于质量改进和保证,但它们几乎适用于任何涉及变异的情况。
在将业务质量改进应用到个人生活的示例中,我最喜欢 Bill Howell 的示例,他将自己的六西格玛专业知识应用于糖尿病的(成功)管理。了解他如何使用《控制图控制血糖》。
我们的一些博主将控制图应用于他们的个人兴趣爱好,包括《控制图:合理子组和 Marshmallow Peeps!》中的假日糖果和《P 控制图问题:不受控的 Cycle LaneYs!》中的自行车骑行。
如果您对运动感兴趣,不妨看看控制图如何揭示《应在何时拦下 NHL 守门员》。或者为照看宇宙而考虑《信噪比:检测外星人和异常因素》。最后,像我这样欲罢不能的读者可能也有兴趣看看控制图与文学的相关性,正如 Cody Steele 在《 Laney P' 控制图展示 Poe 如何在《厄舍古屋的倒塌中创造强度》中所阐述的那样。 最后,想问大家是如何使用控制图的?
查看文章中提及的文章,请评论留言或私信客服。 收起阅读 »
结构化问题解决方法的基础:DMAIC & 8D
在解决问题时,组织希望尽快找到问题的根源。他们还希望确保找到解决该问题的最有效的解决方案,确保该解决方案得到充分实施,并持续到将来,以便该问题不再发生。做到这一点的最好方法是实施结构化的问题解决方案。
在这篇博文中,我们将简要介绍结构化问题解决方案和实现卓越运营的最佳改进方法。
在我们深入研究Minitab的帮助方式之前,让我们先了解一下解决问题的基础知识。
什么是结构化问题解决?
结构化问题解决是一种训练有素的方法,它将问题解决过程分解成具有明确目标的离散步骤。这种方法使你能够处理复杂的问题,同时确保你解决的是正确的问题。它还确保你完全理解这些问题,你已经考虑了合理的解决方案,并有效地实施和维持它们。
什么是结构化的问题解决方法?
结构化问题解决方法是一种由一系列阶段组成的技术,项目在完成之前必须经历这些阶段。方法论的目标是强调解决特定问题背后的意图,并提供解决问题的策略方法。
最好的解决问题的方法是什么?
这取决于你试图为你的改进计划解决的问题。完成每种方法中所有步骤的结构和规则比所选择的特定方法更重要。
为了帮助您轻松直观地了解这些方法,我们创建了问题解决方法周期表。
现在,让我们介绍两种成功的流程改进和问题预防的重要方法:DMAIC和8D.
DMAIC
DMAIC代表“Define,M测量,A分析,I改进和C控制”。DMAIC方法是持续改进和卓越运营中最受欢迎的方法之一。
在进行改进项目时,这种方法提供了一个结构化的五阶段框架。它侧重于改进现有流程,而不是创造新产品或流程。
DMAIC最适合处理复杂的问题,或者风险很高的情况。
8D
8D被称为解决问题的八大纪律。它包括八个步骤来解决困难的、反复出现的或关键的问题。该方法由解决问题的工具组成,帮助您识别、纠正和消除组织中的问题根源。
如果您试图解决的问题很复杂,并且需要快速解决,8D可能是适合您的组织实施的方法。
每种方法都可以用一个项目模板来支持,其中它的路线图对应于该方法中的一组阶段。最佳实践是在进入下一步之前完成给定方法的每一步。
MINITAB ENGAGE,您有效解决问题的解决方案
Minitab Engage铥 旨在帮助组织推动创新和改进计划。我们解决方案的独特之处在于,它将结构化的问题解决方法与工具和仪表盘相结合,帮助您规划、执行和衡量您的创新计划!
有许多解决问题的方法和工具可以帮助你开始。我们拥有终极的端到端改进解决方案,帮助您实现创新成功。 收起阅读 »
在这篇博文中,我们将简要介绍结构化问题解决方案和实现卓越运营的最佳改进方法。
在我们深入研究Minitab的帮助方式之前,让我们先了解一下解决问题的基础知识。
什么是结构化问题解决?
结构化问题解决是一种训练有素的方法,它将问题解决过程分解成具有明确目标的离散步骤。这种方法使你能够处理复杂的问题,同时确保你解决的是正确的问题。它还确保你完全理解这些问题,你已经考虑了合理的解决方案,并有效地实施和维持它们。
什么是结构化的问题解决方法?
结构化问题解决方法是一种由一系列阶段组成的技术,项目在完成之前必须经历这些阶段。方法论的目标是强调解决特定问题背后的意图,并提供解决问题的策略方法。
最好的解决问题的方法是什么?
这取决于你试图为你的改进计划解决的问题。完成每种方法中所有步骤的结构和规则比所选择的特定方法更重要。
为了帮助您轻松直观地了解这些方法,我们创建了问题解决方法周期表。
现在,让我们介绍两种成功的流程改进和问题预防的重要方法:DMAIC和8D.
DMAIC
DMAIC代表“Define,M测量,A分析,I改进和C控制”。DMAIC方法是持续改进和卓越运营中最受欢迎的方法之一。
在进行改进项目时,这种方法提供了一个结构化的五阶段框架。它侧重于改进现有流程,而不是创造新产品或流程。
DMAIC最适合处理复杂的问题,或者风险很高的情况。
8D
8D被称为解决问题的八大纪律。它包括八个步骤来解决困难的、反复出现的或关键的问题。该方法由解决问题的工具组成,帮助您识别、纠正和消除组织中的问题根源。
如果您试图解决的问题很复杂,并且需要快速解决,8D可能是适合您的组织实施的方法。
每种方法都可以用一个项目模板来支持,其中它的路线图对应于该方法中的一组阶段。最佳实践是在进入下一步之前完成给定方法的每一步。
MINITAB ENGAGE,您有效解决问题的解决方案
Minitab Engage铥 旨在帮助组织推动创新和改进计划。我们解决方案的独特之处在于,它将结构化的问题解决方法与工具和仪表盘相结合,帮助您规划、执行和衡量您的创新计划!
有许多解决问题的方法和工具可以帮助你开始。我们拥有终极的端到端改进解决方案,帮助您实现创新成功。 收起阅读 »
用蒙特卡罗模拟增强R&D决策的信心
在做决策的时候,清楚地了解潜在的风险和回报是很重要的。通过使用风险评估和概率建模等工具,个人和组织可以做出更明智的选择,同时将次优结果的可能性降至最低。这通常会带来更好的结果,并促进决策过程中的信心和控制感。
研发团队经常做出代价高昂的决策,因此对他们来说,改进流程以增加积极成果的可能性至关重要。然而,复杂的组织通常使用过于复杂的系统来进行手动优化,这使得优化资源对于带宽和预算来说是不可或缺的。
这就是蒙特卡罗模拟的用武之地。蒙特卡洛模拟是一种非常出色的工具,在准确识别最佳可能结果方面可以发挥很大作用。使用蒙特卡罗模拟,您可以毫不费力地测试数千种或更多的潜在设置,使您能够在定量分析和决策过程中彻底考虑风险。
蒙特卡洛模拟的多功能性还不止于此,这使得它在R&D领域具有不可估量的价值。幸运的是,使用Minitab Workspace访问蒙特卡洛模拟很简单。请继续阅读,了解这一强大工具如何为您的R&D团队带来益处。
R&D的3个主要用途
1.分析风险
估计开发过程中出现延迟的可能性不是很好吗?或者,您可能想要为您想要开发的产品的失败风险建模。
有了蒙特卡洛模拟,你可以提前发现这些障碍,并更有信心地做出预测。利用节省下来的时间,您可以在进行高成本的开发之前集思广益以降低风险,并且您获得的知识在制定开发过程和时间表时非常有价值。
2.优化您的流程
R&D团队可以使用蒙特卡罗模拟来理解复杂的系统和过程。具体来说,您的团队可能能够找出不同过程变量的最佳设置,如压力、温度或流速。这可以帮助您最大限度地提高产品产量和质量,同时节省宝贵的时间和资源。
3.增强您的DOE
在进行DOE后,加入蒙特卡罗模拟可以使你的分析更进一步,使你能够模拟实验和结果。
此外,通过提供对可变性和不确定性的更精确理解,蒙特卡罗模拟可以提高信心,并让您更好地了解当您将产品带到生产车间时会发生什么。这使得生产过程更加可预测,从而减少错误,提高产品质量。
MINITAB为您服务
蒙特卡洛模拟可以通过Minitab Workspace方便地访问。这个强大的工具,以及许多其他工具,可以让你在开始旅程之前,就有能力预测你将会到达哪里。无论您是想分析风险、优化流程、提高DOE还是三者兼而有之,蒙特卡洛模拟都可以帮助您实现目标。 收起阅读 »
研发团队经常做出代价高昂的决策,因此对他们来说,改进流程以增加积极成果的可能性至关重要。然而,复杂的组织通常使用过于复杂的系统来进行手动优化,这使得优化资源对于带宽和预算来说是不可或缺的。
这就是蒙特卡罗模拟的用武之地。蒙特卡洛模拟是一种非常出色的工具,在准确识别最佳可能结果方面可以发挥很大作用。使用蒙特卡罗模拟,您可以毫不费力地测试数千种或更多的潜在设置,使您能够在定量分析和决策过程中彻底考虑风险。
蒙特卡洛模拟的多功能性还不止于此,这使得它在R&D领域具有不可估量的价值。幸运的是,使用Minitab Workspace访问蒙特卡洛模拟很简单。请继续阅读,了解这一强大工具如何为您的R&D团队带来益处。
R&D的3个主要用途
1.分析风险
估计开发过程中出现延迟的可能性不是很好吗?或者,您可能想要为您想要开发的产品的失败风险建模。
有了蒙特卡洛模拟,你可以提前发现这些障碍,并更有信心地做出预测。利用节省下来的时间,您可以在进行高成本的开发之前集思广益以降低风险,并且您获得的知识在制定开发过程和时间表时非常有价值。
2.优化您的流程
R&D团队可以使用蒙特卡罗模拟来理解复杂的系统和过程。具体来说,您的团队可能能够找出不同过程变量的最佳设置,如压力、温度或流速。这可以帮助您最大限度地提高产品产量和质量,同时节省宝贵的时间和资源。
3.增强您的DOE
在进行DOE后,加入蒙特卡罗模拟可以使你的分析更进一步,使你能够模拟实验和结果。
此外,通过提供对可变性和不确定性的更精确理解,蒙特卡罗模拟可以提高信心,并让您更好地了解当您将产品带到生产车间时会发生什么。这使得生产过程更加可预测,从而减少错误,提高产品质量。
MINITAB为您服务
蒙特卡洛模拟可以通过Minitab Workspace方便地访问。这个强大的工具,以及许多其他工具,可以让你在开始旅程之前,就有能力预测你将会到达哪里。无论您是想分析风险、优化流程、提高DOE还是三者兼而有之,蒙特卡洛模拟都可以帮助您实现目标。 收起阅读 »
缩短交付时间,实现更简化的供应链
交货提前期是一个至关重要的供应链管理参数。对于企业来说,了解产品从原始订单到交付需要多长时间是至关重要的,无论他们是购买、销售还是在内部转移货物和材料。
随着消费者越来越习惯于在第二天甚至当天收到订单,供应链越来越关注其流程的交付部分。也就是说,供应链想要保持成功。
我们可以将成功交付定义为在正确的时间以正确的数量获得客户需要的东西,并始终如一地做到这一点。交货现在被认为是任何制造或分销企业最基本的要求。利用数据分析的力量,Minitab可以帮助公司优化交付、简化供应链并提高客户满意度。
衡量交货速度
将最终产品交付给最终客户所需的时间是供应链专业人员的一个关键衡量指标。使用一个样本数据集和一些简单的描述性统计数据,下面的例子显示交付时间的平均值在54到55小时之间。数据还显示最短时间为40小时,最长时间为75小时,因此它提供了最快和最慢时间的范围,这有助于目标设定。
设定一个目标,集体讨论影响交付的可能因素
延迟交付不仅会影响客户体验,还会直接影响销售。如果一家公司不能兑现他们及时交货的承诺,他们的客户将来再次购买的可能性就会大大降低。设定战略性业务目标在一定时间内交货。在本例中,让我们设定一个现实的目标50,这代表交付时间提高了约10%。
接下来,集思广益,找出可能影响交货时间的变量。这可能是包裹大小、车龄、天气状况,甚至是送货的司机。下图显示了一个CT树示例,Workspace中包含的众多强大的头脑风暴和结构化问题解决工具之一。
使用预测模型量化影响…
一般来说,预测建模有助于做出预测以及了解影响响应的因素。通过使用Minitab的自动化机器学习工具,我们不仅能看到最好的模型(在这种情况下随机森林),但我们也能看到其他模特的表现。
在这种情况下,流行的传统回归方法不仅表现最差,而且也不是很准确。然而手推车模型是可视化关系的理想选择,表现相对较好。
应用改进…
通过查看手推车下面的决策树表明,在阳光充足的条件下,新车的交付速度最快,而在下雪天,旧车的交付时间最长。这是第一个需要改进的地方。虽然控制天气状况是不可能的,但维持一个较新的车队可能会带来一些立竿见影的改善。此外,在最初计算和传达交付时间时,考虑特定客户区域的天气预报可以提供更高的准确性。
…并运用模型来预测交货时间
这种分析不仅有助于确定需要改进的地方,还有助于与客户沟通。通过考虑手头的因素,并利用最准确的随机森林模型(由自动机器学习确定),我们可以将模型付诸实施自动与客户交流。使用解决方案,如Minitab模型操作在收集这些数据点时,该模型可以计算估计的交付时间,并自动将时间通知客户。这将确保您的客户及时得到通知,这样他们就不会猜测他们的包裹何时到达。随着您绩效的提高,您不仅可以超额完成客户的期望,还可以继续完善您的预测模型,以便在未来为客户提供更准确的时机。
收起阅读 »
随着消费者越来越习惯于在第二天甚至当天收到订单,供应链越来越关注其流程的交付部分。也就是说,供应链想要保持成功。
我们可以将成功交付定义为在正确的时间以正确的数量获得客户需要的东西,并始终如一地做到这一点。交货现在被认为是任何制造或分销企业最基本的要求。利用数据分析的力量,Minitab可以帮助公司优化交付、简化供应链并提高客户满意度。
衡量交货速度
将最终产品交付给最终客户所需的时间是供应链专业人员的一个关键衡量指标。使用一个样本数据集和一些简单的描述性统计数据,下面的例子显示交付时间的平均值在54到55小时之间。数据还显示最短时间为40小时,最长时间为75小时,因此它提供了最快和最慢时间的范围,这有助于目标设定。
设定一个目标,集体讨论影响交付的可能因素
延迟交付不仅会影响客户体验,还会直接影响销售。如果一家公司不能兑现他们及时交货的承诺,他们的客户将来再次购买的可能性就会大大降低。设定战略性业务目标在一定时间内交货。在本例中,让我们设定一个现实的目标50,这代表交付时间提高了约10%。
接下来,集思广益,找出可能影响交货时间的变量。这可能是包裹大小、车龄、天气状况,甚至是送货的司机。下图显示了一个CT树示例,Workspace中包含的众多强大的头脑风暴和结构化问题解决工具之一。
使用预测模型量化影响…
一般来说,预测建模有助于做出预测以及了解影响响应的因素。通过使用Minitab的自动化机器学习工具,我们不仅能看到最好的模型(在这种情况下随机森林),但我们也能看到其他模特的表现。
在这种情况下,流行的传统回归方法不仅表现最差,而且也不是很准确。然而手推车模型是可视化关系的理想选择,表现相对较好。
应用改进…
通过查看手推车下面的决策树表明,在阳光充足的条件下,新车的交付速度最快,而在下雪天,旧车的交付时间最长。这是第一个需要改进的地方。虽然控制天气状况是不可能的,但维持一个较新的车队可能会带来一些立竿见影的改善。此外,在最初计算和传达交付时间时,考虑特定客户区域的天气预报可以提供更高的准确性。
…并运用模型来预测交货时间
这种分析不仅有助于确定需要改进的地方,还有助于与客户沟通。通过考虑手头的因素,并利用最准确的随机森林模型(由自动机器学习确定),我们可以将模型付诸实施自动与客户交流。使用解决方案,如Minitab模型操作在收集这些数据点时,该模型可以计算估计的交付时间,并自动将时间通知客户。这将确保您的客户及时得到通知,这样他们就不会猜测他们的包裹何时到达。随着您绩效的提高,您不仅可以超额完成客户的期望,还可以继续完善您的预测模型,以便在未来为客户提供更准确的时机。
收起阅读 »
使用Weibull分布对可靠性数据建模
Weibull分布是最常用于对可靠性数据建模的分布。此分布易于解释且用途广泛。在可靠性分析中,可以使用此分布回答以下问题:
· 预计将在老化期间失效的项目所占的百分比是多少?例如,预计将在8小时老化期间失效的保险丝占多大百分比?
· 预计在有效寿命阶段有多少次保修索赔?例如,在该轮胎的50,000英里有效寿命期间预计有多少次保修索赔?
· 预计何时会出现快速磨损?例如,应将维护定期安排在何时以防止发动机进入磨损阶段?
Weibull分布可以对右偏斜数据、左偏斜数据或对称数据建模。因此,分布可用来评估不同应用(包括真空管、电容器、滚珠轴承、继电器和材料强度)的可靠性。Weibull分布还可以对递增、递减或固定故障函数建模,并允许使用该模型描述项目寿命的任何阶段。
Weibull分布参数和故障函数之间的关系
通过调整Weibull分布的形状参数β,可以对许多不同寿命分布的特征建模。
1. 0<β<1
早期失效发生在产品寿命的初始阶段。这些失效可能会迫使产品进入“老化”阶段以降低初期失效的风险。
故障函数:初始失效率很高,随着时间的推移会逐渐降低(“浴盆”形状故障函数的第一部分)。
2. β=1
失效率保持恒定。随机失效,失效的原因有多种。对产品的“使用寿命”建模。
故障函数:失效率在产品寿命期间保持恒定(“浴盆”形状故障函数的第二部分)
3. β=1.5
早期磨损失效
故障函数:失效率不断增加,最初增加速度最快
4. β=2
在产品的寿命期间,磨损失效风险不断增加(当Weibull分布的形状参数为2时,它被称为Rayleigh分布。此分布通常用来描述通信工程领域中的测量数据,如输入回波损耗、调制边带注入、载波抑制和RF衰减的测量数据。此分布还广泛用于电真空设备的寿命检验中。)
故障函数:失效率呈线性增加
5. 3≤β≤4
快速磨损失效。当大多数的失效都出现后,对产品寿命的最后时间段建模。
故障函数:失效率快速增加
6. β>10
非常快的磨损失效。当大多数的磨损失效都出现后,对产品寿命的最后时间段建模。
故障函数:失效率增加速度非常快
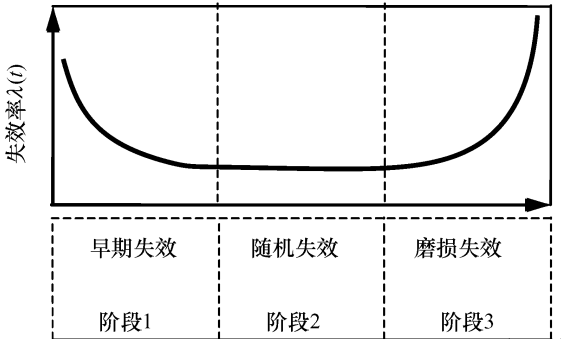
失效率关于时间的图形称为故障图。产品的失效率随时间的变化大致可以分为三个阶段:
早期故障阶段、偶然故障阶段和耗损故障阶段。基于上面介绍,我们发现根据Weibull分布形状参数β的不同,这三个阶段都可以进行描述,于是就形成了如下的“浴盆曲线”。
β<1时,失效率递减,可以描述浴盆曲线的早期故障阶段
β=1时,失效率恒定,可以描述浴盆曲线的偶然故障阶段
β>1时,失效率递增,可以描述浴盆曲线的耗损故障阶段
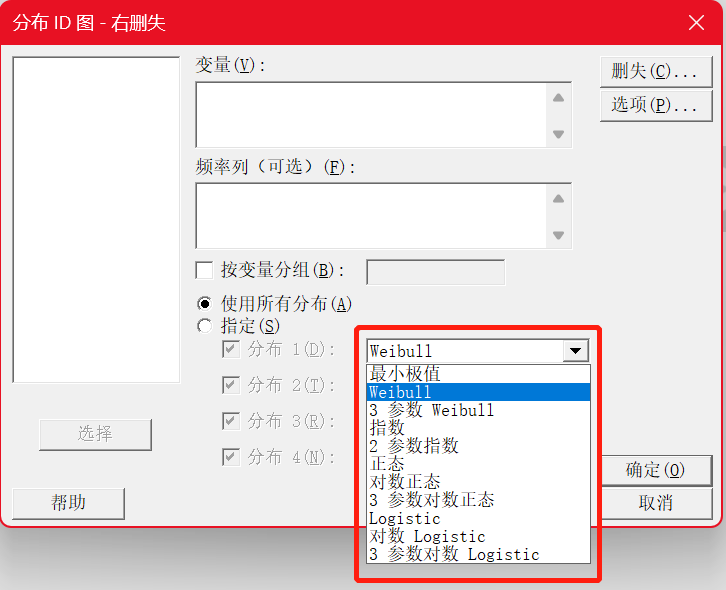
吐槽一下
也可能正是因为Weibull分布看起来很牛,以至于很多朋友把“Weibull”和“可靠性”等价,这其实是有问题的。Minitab中可靠性分析分布其实有11种,而Weibull分布只是其中一种而已,并不是所有寿命数据用Weibull都能拟合的很好。
收起阅读 »
· 预计将在老化期间失效的项目所占的百分比是多少?例如,预计将在8小时老化期间失效的保险丝占多大百分比?
· 预计在有效寿命阶段有多少次保修索赔?例如,在该轮胎的50,000英里有效寿命期间预计有多少次保修索赔?
· 预计何时会出现快速磨损?例如,应将维护定期安排在何时以防止发动机进入磨损阶段?
Weibull分布可以对右偏斜数据、左偏斜数据或对称数据建模。因此,分布可用来评估不同应用(包括真空管、电容器、滚珠轴承、继电器和材料强度)的可靠性。Weibull分布还可以对递增、递减或固定故障函数建模,并允许使用该模型描述项目寿命的任何阶段。
Weibull分布参数和故障函数之间的关系
通过调整Weibull分布的形状参数β,可以对许多不同寿命分布的特征建模。
1. 0<β<1
早期失效发生在产品寿命的初始阶段。这些失效可能会迫使产品进入“老化”阶段以降低初期失效的风险。
故障函数:初始失效率很高,随着时间的推移会逐渐降低(“浴盆”形状故障函数的第一部分)。
2. β=1
失效率保持恒定。随机失效,失效的原因有多种。对产品的“使用寿命”建模。
故障函数:失效率在产品寿命期间保持恒定(“浴盆”形状故障函数的第二部分)
3. β=1.5
早期磨损失效
故障函数:失效率不断增加,最初增加速度最快
4. β=2
在产品的寿命期间,磨损失效风险不断增加(当Weibull分布的形状参数为2时,它被称为Rayleigh分布。此分布通常用来描述通信工程领域中的测量数据,如输入回波损耗、调制边带注入、载波抑制和RF衰减的测量数据。此分布还广泛用于电真空设备的寿命检验中。)
故障函数:失效率呈线性增加
5. 3≤β≤4
快速磨损失效。当大多数的失效都出现后,对产品寿命的最后时间段建模。
故障函数:失效率快速增加
6. β>10
非常快的磨损失效。当大多数的磨损失效都出现后,对产品寿命的最后时间段建模。
故障函数:失效率增加速度非常快
失效率关于时间的图形称为故障图。产品的失效率随时间的变化大致可以分为三个阶段:
早期故障阶段、偶然故障阶段和耗损故障阶段。基于上面介绍,我们发现根据Weibull分布形状参数β的不同,这三个阶段都可以进行描述,于是就形成了如下的“浴盆曲线”。
β<1时,失效率递减,可以描述浴盆曲线的早期故障阶段
β=1时,失效率恒定,可以描述浴盆曲线的偶然故障阶段
β>1时,失效率递增,可以描述浴盆曲线的耗损故障阶段
吐槽一下
也可能正是因为Weibull分布看起来很牛,以至于很多朋友把“Weibull”和“可靠性”等价,这其实是有问题的。Minitab中可靠性分析分布其实有11种,而Weibull分布只是其中一种而已,并不是所有寿命数据用Weibull都能拟合的很好。
收起阅读 »
制造业的数字化转型:机遇、挑战和经验教训
Greg Kinsey是卓越运营、数字化转型和工业 4.0 领域的高级顾问,帮助工业公司制定工业 4.0 战略、实施、利益相关者的支持和调整、Genba 参与和收益实现。2023 年 1 月,他作为合伙人加入国际运营咨询公司和 Minitab Gold Level 咨询公司Argon & Co,领导数字制造实践。
在 2022 年 9 月 20 日于慕尼黑举行的 Minitab Exchange 活动中,Greg 分享了他的经验以及制造领导者通过数字化日常运营以提高绩效的旅程中的主要经验教训。格雷格描述了公司面临的最常见挑战以及他对解决这些挑战的建议。
数字化转型将带来第四次工业革命
如果你回到 1800 年代的工厂,在第一次工业革命期间,你会发现工匠——高技能的人从事专业化工作,几乎没有标准化。
第二次工业革命迎来了标准化工作。具有特定技能、重复特定任务、专门从事装配操作的指定方面的人员。这是管理和控制过程的一种新的科学方法。泰勒主义和福特主义为制造业带来了新的工作方式。
第三次工业革命引入了持续改进和质量体系的概念,以及新的 IT 和 OT 系统。工人们开始与自动化生产并肩工作,并获得了更大的自主权和对结果的责任。这引入了用于解决问题和控制过程变化的六西格码方法,以及所谓的丰田生产系统或精益管理。
第四次工业革命将带来根本性的变化,因为我们将在更多的知识基础上工作。在大多数情况下,工人不会从事体力劳动,但他们将通过知识管理体力劳动。他们创造的价值将基于他们的知识,以及他们如何将数据整合在一起以优化生产力、解决问题、监控流程和管理运营。
制造商的数字化转型机会是什么?
当我们谈论数字化转型时,它是关于改进工作方式。它是关于使用数字工具从根本上实现现代化并改善工人、管理人员的日常生活和工厂的绩效。如果我们考虑一下这种变化是什么样的,那就是从一种反应性制造文化转变为一种更具预测性和可控性……以及数据驱动的文化。
传统上,制造业以灭火和不断解决问题为主。有了数字工厂的愿景,您可以更好地了解未来会发生什么。您可以更好地预测您的流程在未来将如何执行,这意味着您可以以更可控的方式管理您的制造。它还涉及从分散的运营模式转变为更加集成的模式。无论是数据孤岛、人员孤岛还是流程孤岛——我们都需要更多相互联系的团队和流程上下一致的数据定义。
这还涉及从基于过去发生的事情进行操作的历史知识转变为可以预测未来会发生什么的智能工厂。因此,由于流程中内置的智能,我们拥有更大的灵活性,而不是拥有一个流程、机器和人员都是固定的环境。
数字化转型面临哪些主要挑战?
(1)关注问题,而不是解决方案
我看到公司经常犯的第一个错误是他们忽视了他们想要解决的问题。很多时候,解决方案是推动投资而不是解决问题。专注于您想要解决的问题的最佳方法之一是将您的数字计划与您的卓越运营计划联系起来。
如果您有像精益六西格码黑带这样的项目负责人和问题解决者,那么他们已经有了一系列他们正在努力解决的问题。与其尝试安装新软件,不如考虑数字技术如何补充和加速已经在进行的问题解决。
(2)收集数据
另一大挑战是数据采集。收集正确的数据可能是一个耗时的过程,而且它可能以不同的格式分散在不同的地方。您可能混合使用旧机器和新机器——有些有数据端口,有些则没有。您如何连接所有这些可能具有不同网络和协议的不同可编程控制器?您可能不会到处都有传感器,您的愿景可能需要您拥有更多的物联网设备。
说到数据,清理时间总是比我们预期的要长。我建议构建一个数据字典——一种标记和分类数据的方法。这将为您提供描述其中内容的数据周围的元数据,使其更易于有效使用。
(3)对未来没有清晰的愿景
公司应关注的另一个领域是创建清晰的路线图并确定未来的架构以实现其目标。五年或十年后你的工厂会是什么样子?您的技术选择可能很困难,而且 IT 系统中的遗留问题会受到一些限制。构建可扩展的架构非常重要,这样您就不会构建过时的东西。
(4)项目管理的经典方法
数字化转型使用的方法与传统 IT 项目不同——事实上,恰恰相反。传统 IT 是将已知解决方案应用于已知问题,您的 IT 系统可能看起来与竞争对手部署的系统非常相似。数字创新是关于使用敏捷流程建立数据库并开发定制解决方案,以应用机器学习、人工智能或高级分析来解决您的特定问题。根据定义,它是创新,而不是现成的解决方案。
(5)缺乏管理层的参与和协调
最大的挑战之一是如何吸引员工。通常,质量经理会有一个议程,但物流经理可能有不同的痛点。问工厂经理他们需要什么,这可能是一个完全不同的故事。关键是使您的卓越运营职能与数字职能保持一致,以便每个人都围绕目标以及如何实现目标保持一致并参与其中。
(6)忽略Genba
经验表明,最好的想法来自于在创造价值的领域 (Genba) 工作的人。他们了解流程如何运作以及机器如何运作。如果您问人们如何通过应用数字工具来改善事物,他们通常会提出很多想法,因为他们想要使工作场所现代化。如果他们参与构思过程,他们也会有一种主人翁感。他们为自己的贡献感到自豪,并热衷于帮助推动项目完成。
(7)没有利益实现
我听到的最重要的事情之一是,“我们尝试了概念验证,但没有产生任何结果。” 如果您得不到这些好处,无法实现速赢,您将无法继续您的旅程。专注于确保获得这些结果,当你这样做时,在财务的帮助下验证这些结果。传达项目结果及其带来价值的原因。
您从制造业的数字化转型中学到了哪些经验教训?
(1)整合必不可少
您的卓越运营计划必须与您的数字化转型计划相结合。数字化转型只是卓越运营的下一阶段,如果您不将精益六西格码计划带入数字世界,它就会过时。
(2)最小可行数据集
您无需构建海量数据湖。首先从解决特定问题所需的最小数据集开始。专注于一个用例和为此目的所需的数据——您可以随时添加更多。
(3)允许试错
在敏捷工程中,您希望进行创新并允许进行实验。不要害怕快速失败并从中学习。不要害怕根据你从这些失败中学到的东西来调整你的方向。
(4)保持好奇
你无法购买现成的智能工厂,你必须自己发明。如果您想超越竞争对手进行创新,请特别是在您的行业之外寻找新想法。
预测分析在第四次工业革命中扮演什么角色?
制造业以反动着称,人们总是“救火”并修理意外损坏的东西。我认为数字化转型的承诺是创造一个更主动、更可控的环境,在这个环境中,您可以轻松了解正在发生的事情。您掌中的手机成为您高效开展日常工作所需的主要信息来源。根据数据,在问题发生之前警告您。这减少了消防工作,减轻了压力,并让人们自信地掌控一切。
数据驱动这个词可能被滥用了。但是,当人们在需要解决问题或进行调整时可以获得仪表板和可视化效果来帮助他们做出数据驱动的决策时,这将改变他们日常工作的本质。当这些人不仅仅是坐在办公室里的高管时,革命就来了——它也是 Genba 中的司机、机器操作员、质量经理和维护人员。当 Genba 的劳动力可以从数据驱动的工作环境中受益时,也许我们已经迎来了第四次工业革命。 收起阅读 »
在 2022 年 9 月 20 日于慕尼黑举行的 Minitab Exchange 活动中,Greg 分享了他的经验以及制造领导者通过数字化日常运营以提高绩效的旅程中的主要经验教训。格雷格描述了公司面临的最常见挑战以及他对解决这些挑战的建议。
数字化转型将带来第四次工业革命
如果你回到 1800 年代的工厂,在第一次工业革命期间,你会发现工匠——高技能的人从事专业化工作,几乎没有标准化。
第二次工业革命迎来了标准化工作。具有特定技能、重复特定任务、专门从事装配操作的指定方面的人员。这是管理和控制过程的一种新的科学方法。泰勒主义和福特主义为制造业带来了新的工作方式。
第三次工业革命引入了持续改进和质量体系的概念,以及新的 IT 和 OT 系统。工人们开始与自动化生产并肩工作,并获得了更大的自主权和对结果的责任。这引入了用于解决问题和控制过程变化的六西格码方法,以及所谓的丰田生产系统或精益管理。
第四次工业革命将带来根本性的变化,因为我们将在更多的知识基础上工作。在大多数情况下,工人不会从事体力劳动,但他们将通过知识管理体力劳动。他们创造的价值将基于他们的知识,以及他们如何将数据整合在一起以优化生产力、解决问题、监控流程和管理运营。
制造商的数字化转型机会是什么?
当我们谈论数字化转型时,它是关于改进工作方式。它是关于使用数字工具从根本上实现现代化并改善工人、管理人员的日常生活和工厂的绩效。如果我们考虑一下这种变化是什么样的,那就是从一种反应性制造文化转变为一种更具预测性和可控性……以及数据驱动的文化。
传统上,制造业以灭火和不断解决问题为主。有了数字工厂的愿景,您可以更好地了解未来会发生什么。您可以更好地预测您的流程在未来将如何执行,这意味着您可以以更可控的方式管理您的制造。它还涉及从分散的运营模式转变为更加集成的模式。无论是数据孤岛、人员孤岛还是流程孤岛——我们都需要更多相互联系的团队和流程上下一致的数据定义。
这还涉及从基于过去发生的事情进行操作的历史知识转变为可以预测未来会发生什么的智能工厂。因此,由于流程中内置的智能,我们拥有更大的灵活性,而不是拥有一个流程、机器和人员都是固定的环境。
数字化转型面临哪些主要挑战?
(1)关注问题,而不是解决方案
我看到公司经常犯的第一个错误是他们忽视了他们想要解决的问题。很多时候,解决方案是推动投资而不是解决问题。专注于您想要解决的问题的最佳方法之一是将您的数字计划与您的卓越运营计划联系起来。
如果您有像精益六西格码黑带这样的项目负责人和问题解决者,那么他们已经有了一系列他们正在努力解决的问题。与其尝试安装新软件,不如考虑数字技术如何补充和加速已经在进行的问题解决。
(2)收集数据
另一大挑战是数据采集。收集正确的数据可能是一个耗时的过程,而且它可能以不同的格式分散在不同的地方。您可能混合使用旧机器和新机器——有些有数据端口,有些则没有。您如何连接所有这些可能具有不同网络和协议的不同可编程控制器?您可能不会到处都有传感器,您的愿景可能需要您拥有更多的物联网设备。
说到数据,清理时间总是比我们预期的要长。我建议构建一个数据字典——一种标记和分类数据的方法。这将为您提供描述其中内容的数据周围的元数据,使其更易于有效使用。
(3)对未来没有清晰的愿景
公司应关注的另一个领域是创建清晰的路线图并确定未来的架构以实现其目标。五年或十年后你的工厂会是什么样子?您的技术选择可能很困难,而且 IT 系统中的遗留问题会受到一些限制。构建可扩展的架构非常重要,这样您就不会构建过时的东西。
(4)项目管理的经典方法
数字化转型使用的方法与传统 IT 项目不同——事实上,恰恰相反。传统 IT 是将已知解决方案应用于已知问题,您的 IT 系统可能看起来与竞争对手部署的系统非常相似。数字创新是关于使用敏捷流程建立数据库并开发定制解决方案,以应用机器学习、人工智能或高级分析来解决您的特定问题。根据定义,它是创新,而不是现成的解决方案。
(5)缺乏管理层的参与和协调
最大的挑战之一是如何吸引员工。通常,质量经理会有一个议程,但物流经理可能有不同的痛点。问工厂经理他们需要什么,这可能是一个完全不同的故事。关键是使您的卓越运营职能与数字职能保持一致,以便每个人都围绕目标以及如何实现目标保持一致并参与其中。
(6)忽略Genba
经验表明,最好的想法来自于在创造价值的领域 (Genba) 工作的人。他们了解流程如何运作以及机器如何运作。如果您问人们如何通过应用数字工具来改善事物,他们通常会提出很多想法,因为他们想要使工作场所现代化。如果他们参与构思过程,他们也会有一种主人翁感。他们为自己的贡献感到自豪,并热衷于帮助推动项目完成。
(7)没有利益实现
我听到的最重要的事情之一是,“我们尝试了概念验证,但没有产生任何结果。” 如果您得不到这些好处,无法实现速赢,您将无法继续您的旅程。专注于确保获得这些结果,当你这样做时,在财务的帮助下验证这些结果。传达项目结果及其带来价值的原因。
您从制造业的数字化转型中学到了哪些经验教训?
(1)整合必不可少
您的卓越运营计划必须与您的数字化转型计划相结合。数字化转型只是卓越运营的下一阶段,如果您不将精益六西格码计划带入数字世界,它就会过时。
(2)最小可行数据集
您无需构建海量数据湖。首先从解决特定问题所需的最小数据集开始。专注于一个用例和为此目的所需的数据——您可以随时添加更多。
(3)允许试错
在敏捷工程中,您希望进行创新并允许进行实验。不要害怕快速失败并从中学习。不要害怕根据你从这些失败中学到的东西来调整你的方向。
(4)保持好奇
你无法购买现成的智能工厂,你必须自己发明。如果您想超越竞争对手进行创新,请特别是在您的行业之外寻找新想法。
预测分析在第四次工业革命中扮演什么角色?
制造业以反动着称,人们总是“救火”并修理意外损坏的东西。我认为数字化转型的承诺是创造一个更主动、更可控的环境,在这个环境中,您可以轻松了解正在发生的事情。您掌中的手机成为您高效开展日常工作所需的主要信息来源。根据数据,在问题发生之前警告您。这减少了消防工作,减轻了压力,并让人们自信地掌控一切。
数据驱动这个词可能被滥用了。但是,当人们在需要解决问题或进行调整时可以获得仪表板和可视化效果来帮助他们做出数据驱动的决策时,这将改变他们日常工作的本质。当这些人不仅仅是坐在办公室里的高管时,革命就来了——它也是 Genba 中的司机、机器操作员、质量经理和维护人员。当 Genba 的劳动力可以从数据驱动的工作环境中受益时,也许我们已经迎来了第四次工业革命。 收起阅读 »
持续改进的基础和原则
每个组织都想改进。无论行业或部门,每个人都希望向卓越业务稳步变革。
在这篇博文中,我们将重点介绍持续改进的基础知识、阶段和原则,以帮助您确保在整个组织中成功实施 CI。如果您不熟悉持续改进,Minitab Engage提供了帮助您入门的工具。
什么是持续改进?
持续改进 (CI)是在整个组织中改进流程、产品或服务的持续努力。该概念侧重于加强为客户创造最大价值的活动,同时消除浪费并提高组织效率。
CI 可以帮助组织解决以下任何挑战:
• 缺乏对计划的即时和完整可见性
• 难以执行和维持卓越运营
• 难以获得利益相关者的支持
• 无法创建可衡量的创新文化
持续改进就是持续的。组织定期寻求进行渐进式改进,并确保它们是渐进式的可以使它们更容易实现。
持续改进的 4 个阶段
您可能还听说过称为PDCA 循环或计划-执行-检查-行动的持续改进,它支持持续改进的四个步骤。
阶段 1.计划:确定流程目标和实现这些目标所需的更改
阶段 2.执行:实施这些更改
阶段 3.检查:评估绩效
阶段 4.行动:标准化并稳定该更改,或重新开始循环
这种重复的循环是持续改进的基础。
PDCA 循环是 CI 流程从开始到结束的高级视图。我们还想指出,PDCA也指一种流行的同名问题解决方法。该方法用于通过将流程或产品分解为步骤并改进每个步骤来改进流程或产品。通过实施解决问题的方法,组织可以尽快有效地找到他们试图解决的问题的根源。
持续改进的原则
现在我们已经介绍了持续改进的基础知识,让我们深入探讨这些原则。这些原则将帮助您更好地理解您要解决的问题,从而更有效地解决它们。
让Minitab Engage成为您持续改进计划的首选解决方案。 收起阅读 »
在这篇博文中,我们将重点介绍持续改进的基础知识、阶段和原则,以帮助您确保在整个组织中成功实施 CI。如果您不熟悉持续改进,Minitab Engage提供了帮助您入门的工具。
什么是持续改进?
持续改进 (CI)是在整个组织中改进流程、产品或服务的持续努力。该概念侧重于加强为客户创造最大价值的活动,同时消除浪费并提高组织效率。
CI 可以帮助组织解决以下任何挑战:
• 缺乏对计划的即时和完整可见性
• 难以执行和维持卓越运营
• 难以获得利益相关者的支持
• 无法创建可衡量的创新文化
持续改进就是持续的。组织定期寻求进行渐进式改进,并确保它们是渐进式的可以使它们更容易实现。
持续改进的 4 个阶段
您可能还听说过称为PDCA 循环或计划-执行-检查-行动的持续改进,它支持持续改进的四个步骤。
阶段 1.计划:确定流程目标和实现这些目标所需的更改
阶段 2.执行:实施这些更改
阶段 3.检查:评估绩效
阶段 4.行动:标准化并稳定该更改,或重新开始循环
这种重复的循环是持续改进的基础。
PDCA 循环是 CI 流程从开始到结束的高级视图。我们还想指出,PDCA也指一种流行的同名问题解决方法。该方法用于通过将流程或产品分解为步骤并改进每个步骤来改进流程或产品。通过实施解决问题的方法,组织可以尽快有效地找到他们试图解决的问题的根源。
持续改进的原则
现在我们已经介绍了持续改进的基础知识,让我们深入探讨这些原则。这些原则将帮助您更好地理解您要解决的问题,从而更有效地解决它们。
让Minitab Engage成为您持续改进计划的首选解决方案。 收起阅读 »
R-sq越高代表模型拟合越好?
在统计建模中,究竟R-sq应该取多大? 我们经常听到这个疑问。以前,我们分享过如何解释R-Sq,我们还纠正了一个统计上的误区,即较低的R-sq不一定差,较高的R-sq不一定好。显然,“R-sq应该多高”的答案就是:视情况而定。
盲目追求高R-sq的模型很容易掉入过度拟合的陷阱,这一点在大数据建模中经常发现。
什么是好的模型?
我们在建模的时候最不愿意看到两种情况:过度拟合和欠拟合。使用与拟合模型相同的数据来评估模型,经常会导致过度拟合,如下图:
而这种过度拟合的模型如果用来预测的话,效果往往不好。
那么什么才算一个好的模型呢?一个好的模型需要在高方差(过度拟合)和高偏差(欠拟合)之间找到一种权衡。
上图就是由于模型太简单导致存在高的偏差。
上图就是由于模型过度拟合导致存在高的方差。
过度拟合与欠拟合之间的权衡
那么如何去找到“高偏差”与“高方差”之间的权衡呢?这就需要用到“验证”法了。
大数据建模把数据分为两大类:训练集和测试集。训练集用来创建模型,而测试集来评估模型的性能,这样我们就可以来权衡过度拟合和欠拟合的模型。
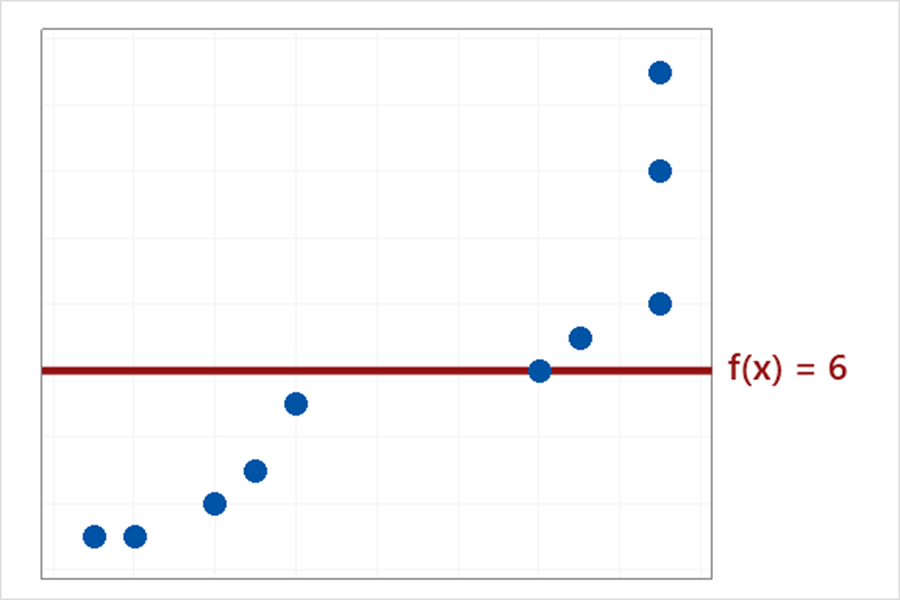
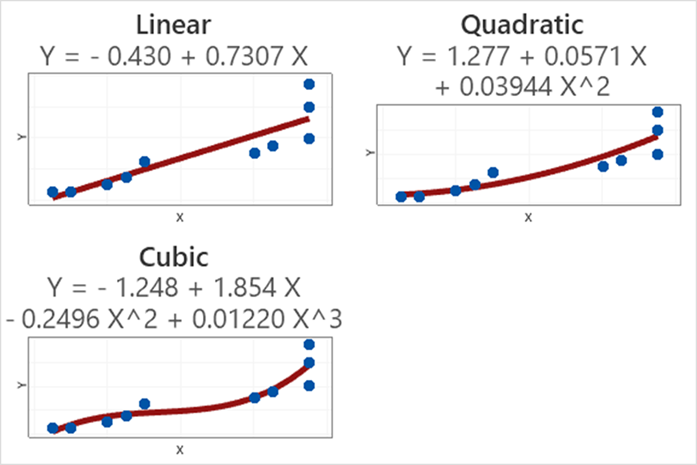
举个例子,对于同一组数据我们可以下面三个不同的模型,看起来立方模型是最好的。
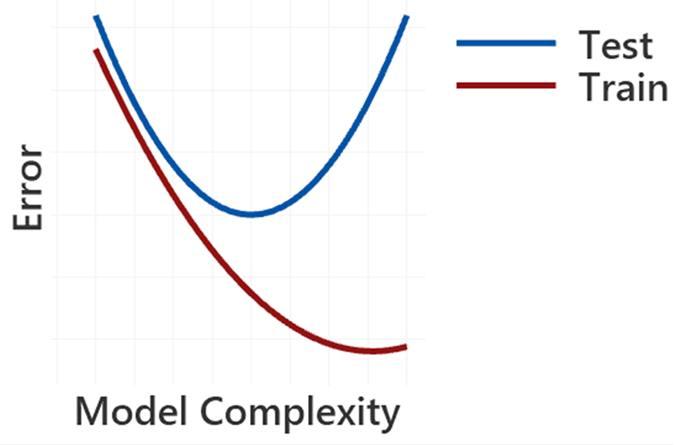
但当我们常用验证法,从下图中我们可知,用训练集来建模时,模型越复杂模型误差确实越小,但再来看看测试集你会发现当模型复杂到一定程度,它的误差会随着模型复杂度的增加而增大。也就是说,太简单和太复杂的模型都不能很好的用来预测。看来找到这个权衡点很重要,这是如何做到的呢?这就要来说说所谓的“验证”法了。
三种验证方法
在Minitab 21版本的回归(拟合回归模型、拟合二值Logistic模型、拟合Poisson模型)和预测分析模块中包含三种用于验证的方法:
对这三种验证方法做一个简单介绍:
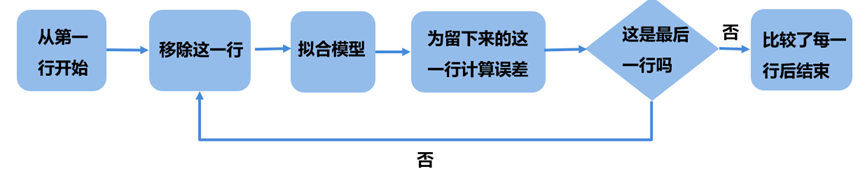
1. 留一验证法
这种方法正如其名,留一留一,就是留下一行yi,再用其他所有数据来建模,得到模型后再把留下来这一行代入得到的模型就会得到对应的拟合者,其过程如下所示:
接下来,我们计算预测的残差平方和(Predicted Residual Sum of Squares)
有了PRESS就可以来计算R-sq(预测)了,到这里是不是很熟悉了。
2. 测试集验证法
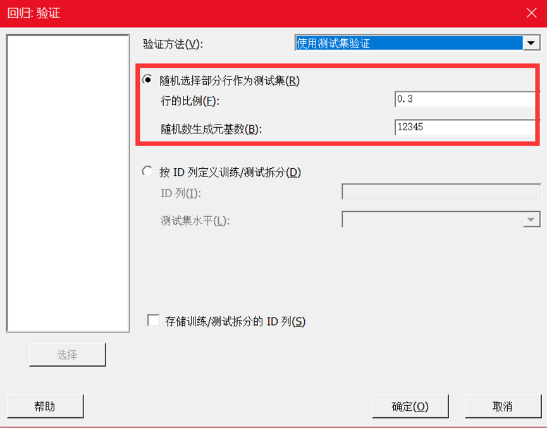
随机保留一定比例(Minitab 21默认保留30%)的数据(测试集),用剩余的数据来拟合模型(训练集)。
3. K折交叉验证法
将数据拆分个K个子集,以其中一份为测试数据,其它K-1份用于训练数据来拟合模型。使用测试数据计算误差,重复k次,每次忽略一份,基于测试数据误差统计汇总信息选择模型。
小结
当你询问R-sq应该取多大时,可能是因为你想确定当前模型是否能够满足要求。我希望你有更好的方法来解决这这个问题而不是只通过R-sq,尤其当你的数据量和数据维度比较大的时候。 收起阅读 »
盲目追求高R-sq的模型很容易掉入过度拟合的陷阱,这一点在大数据建模中经常发现。
什么是好的模型?
我们在建模的时候最不愿意看到两种情况:过度拟合和欠拟合。使用与拟合模型相同的数据来评估模型,经常会导致过度拟合,如下图:
而这种过度拟合的模型如果用来预测的话,效果往往不好。
那么什么才算一个好的模型呢?一个好的模型需要在高方差(过度拟合)和高偏差(欠拟合)之间找到一种权衡。
上图就是由于模型太简单导致存在高的偏差。
上图就是由于模型过度拟合导致存在高的方差。
过度拟合与欠拟合之间的权衡
那么如何去找到“高偏差”与“高方差”之间的权衡呢?这就需要用到“验证”法了。
大数据建模把数据分为两大类:训练集和测试集。训练集用来创建模型,而测试集来评估模型的性能,这样我们就可以来权衡过度拟合和欠拟合的模型。
举个例子,对于同一组数据我们可以下面三个不同的模型,看起来立方模型是最好的。
但当我们常用验证法,从下图中我们可知,用训练集来建模时,模型越复杂模型误差确实越小,但再来看看测试集你会发现当模型复杂到一定程度,它的误差会随着模型复杂度的增加而增大。也就是说,太简单和太复杂的模型都不能很好的用来预测。看来找到这个权衡点很重要,这是如何做到的呢?这就要来说说所谓的“验证”法了。
三种验证方法
在Minitab 21版本的回归(拟合回归模型、拟合二值Logistic模型、拟合Poisson模型)和预测分析模块中包含三种用于验证的方法:
对这三种验证方法做一个简单介绍:
1. 留一验证法
这种方法正如其名,留一留一,就是留下一行yi,再用其他所有数据来建模,得到模型后再把留下来这一行代入得到的模型就会得到对应的拟合者,其过程如下所示:
接下来,我们计算预测的残差平方和(Predicted Residual Sum of Squares)
有了PRESS就可以来计算R-sq(预测)了,到这里是不是很熟悉了。
2. 测试集验证法
随机保留一定比例(Minitab 21默认保留30%)的数据(测试集),用剩余的数据来拟合模型(训练集)。
3. K折交叉验证法
将数据拆分个K个子集,以其中一份为测试数据,其它K-1份用于训练数据来拟合模型。使用测试数据计算误差,重复k次,每次忽略一份,基于测试数据误差统计汇总信息选择模型。
小结
当你询问R-sq应该取多大时,可能是因为你想确定当前模型是否能够满足要求。我希望你有更好的方法来解决这这个问题而不是只通过R-sq,尤其当你的数据量和数据维度比较大的时候。 收起阅读 »
制造业高效节能的 3 大数据驱动策略
随着能源成本的稳步上升,一些组织感到有压力主动制定策略来减少能源消耗。
据路透社报道,能效措施对于进一步支持脱碳工作和减少能源使用仍然至关重要,尤其是在钢铁、水泥和石化等能源密集型行业。文章还指出,通过详细了解能源消耗并制定减少能源消耗的战略,公司可以投资于通常会带来显着回报的具有成本效益的措施。
组织如何才能成功节约能源?
借助由数据驱动的决策支持的良好行动计划,企业可以发现宝贵的节约机会,以减少碳足迹。在这篇博文中,我们介绍了帮助您实现高效节能的三个主要策略,以及帮助您实现可持续发展成功的 Minitab 解决方案。让我们从第一个策略开始。
策略 1:使用部分回收材料进行制造
Signify 是照明技术领域的全球领导者,致力于通过推动环保解决方案的发展,为更可持续的未来做出贡献。这包括可以重印或翻新的制造产品,以及专门为保护工作重新使用材料的服务。
例如,灯回收通过减少资源开采的电力使用使人类基础设施受益。这也通过减少资源稀缺对环境产生影响。通过专门的处理设施,超过 80% 的灯可回收材料可以重复使用,在促进全球生态保护实践的同时提供了大量的经济机会。
现实生活中的用例
为了保持他们的可持续发展努力,Signify 开始使用部分回收材料来 3D 打印照明材料。他们的目标是在使用回收材料和节约能源的同时,尽快向客户提供印刷产品。
通过使用Minitab Engage中提供的 House of Quality以及数据分析Minitab,Signify 能够定制他们的照明材料,不仅可以满足客户的需求,还可以更快地发布为循环经济设计的产品,并增加能源效率。此外,Signify 还降低了他们的故障率并每年节省了大量的非机密成本。
接下来,我们将重点介绍管理能源浪费的方法。
策略 2:维护设备以消除能源浪费
造成能源浪费的可能原因之一是设备维护不当。例如,由于对齐问题或轴承损坏,电机可能会发热。
为了减少能源消耗,组织可以执行以下任何操作:
1. 定期检查他们工厂的设备和设备
2. 确定最有效的维护、升级和更换方法
3. 在特定时间内将设备置于低能耗模式
除了设备计划外,采用有效的预防性维护方法对于最大限度地节省成本也是必不可少的。预测性维护技术有助于预测设备维护需求。
有关材料退化的知识以及有关工艺和设备的数据,将为您的团队提供有关设备可靠性的宝贵信息。一个项目的可靠性是它在指定的环境条件下,在指定的时间段内充分执行其指定目的的概率。幸运的是,Minitab具有可靠性测试,可以确定零件、产品和设备的寿命和故障风险。
现实生活中的用例
一家商用飞机制造商希望减少特定喷气发动机软管的停机时间。通过使用 Minitab 软件,他们希望通过在 282 天内安排零件更换来预测其可靠性。
运行分析后,制造商确定柔性软管至少可以使用 282.4 天。在该时间范围之前安排更换可减少计划外维护和停机时间,从而为制造商节省大量成本。
通过利用从他们的分析中收集到的数据,团队可以通过先进的图形和定量分析技术自信地预测产品寿命和可靠性。通过这样做,他们会在潜在的机械故障发生之前更加安全地了解它们。这些见解将帮助他们评估与设计或目标相关的能源效率低下的风险,并预测优化结果 - 同时快速高效地工作。
最后,我们将介绍我们的第三个能源消耗策略。
策略 3:定期监控您的流程和材料
优化能源效率的另一种方法是定期监控工厂的流程和材料。这允许跨团队进行改进,以查明根本原因并简化整个组织的问题解决。
现实生活中的用例
世界上最大的太阳能技术和可再生能源公司之一在发现其制造过程中存在不一致后,需要控制氮化硅薄膜的厚度。
使用Minitab 和 Minitab Engage™中提供的强大图表和分析工具,该公司能够查明并纠正薄膜厚度差异的原因。
借助 Minitab 强大的分析和改进解决方案,该制造商能够将其面板的能源效率提高7%,并将其年收入增加超过100,000 美元/年。
在对制造过程应用更改之前,已发布产品的质量需要保持一致。Minitab 拥有可确保您的产品质量满足客户期望并符合监管标准的解决方案。
其他需要考虑的例子:
1.如果您希望在投资成本和能源效率之间进行权衡分析,Minitab 中的Graph Builder将是一个很好的解决方案。
2.Minitab Engage 中可用的DMAIC项目可用于跟踪改进,而 Monte Carlo 可用于模拟针对您的计划提出的更改。
结论
这些只是您的组织可以实施以实现节能成功的众多策略中的一小部分。从数据中获得的见解可以帮助您确定最适合您的业务的策略,而 Minitab 是您实现能源效率的端到端分析和 CI 解决方案。 收起阅读 »
据路透社报道,能效措施对于进一步支持脱碳工作和减少能源使用仍然至关重要,尤其是在钢铁、水泥和石化等能源密集型行业。文章还指出,通过详细了解能源消耗并制定减少能源消耗的战略,公司可以投资于通常会带来显着回报的具有成本效益的措施。
组织如何才能成功节约能源?
借助由数据驱动的决策支持的良好行动计划,企业可以发现宝贵的节约机会,以减少碳足迹。在这篇博文中,我们介绍了帮助您实现高效节能的三个主要策略,以及帮助您实现可持续发展成功的 Minitab 解决方案。让我们从第一个策略开始。
策略 1:使用部分回收材料进行制造
Signify 是照明技术领域的全球领导者,致力于通过推动环保解决方案的发展,为更可持续的未来做出贡献。这包括可以重印或翻新的制造产品,以及专门为保护工作重新使用材料的服务。
例如,灯回收通过减少资源开采的电力使用使人类基础设施受益。这也通过减少资源稀缺对环境产生影响。通过专门的处理设施,超过 80% 的灯可回收材料可以重复使用,在促进全球生态保护实践的同时提供了大量的经济机会。
现实生活中的用例
为了保持他们的可持续发展努力,Signify 开始使用部分回收材料来 3D 打印照明材料。他们的目标是在使用回收材料和节约能源的同时,尽快向客户提供印刷产品。
通过使用Minitab Engage中提供的 House of Quality以及数据分析Minitab,Signify 能够定制他们的照明材料,不仅可以满足客户的需求,还可以更快地发布为循环经济设计的产品,并增加能源效率。此外,Signify 还降低了他们的故障率并每年节省了大量的非机密成本。
接下来,我们将重点介绍管理能源浪费的方法。
策略 2:维护设备以消除能源浪费
造成能源浪费的可能原因之一是设备维护不当。例如,由于对齐问题或轴承损坏,电机可能会发热。
为了减少能源消耗,组织可以执行以下任何操作:
1. 定期检查他们工厂的设备和设备
2. 确定最有效的维护、升级和更换方法
3. 在特定时间内将设备置于低能耗模式
除了设备计划外,采用有效的预防性维护方法对于最大限度地节省成本也是必不可少的。预测性维护技术有助于预测设备维护需求。
有关材料退化的知识以及有关工艺和设备的数据,将为您的团队提供有关设备可靠性的宝贵信息。一个项目的可靠性是它在指定的环境条件下,在指定的时间段内充分执行其指定目的的概率。幸运的是,Minitab具有可靠性测试,可以确定零件、产品和设备的寿命和故障风险。
现实生活中的用例
一家商用飞机制造商希望减少特定喷气发动机软管的停机时间。通过使用 Minitab 软件,他们希望通过在 282 天内安排零件更换来预测其可靠性。
运行分析后,制造商确定柔性软管至少可以使用 282.4 天。在该时间范围之前安排更换可减少计划外维护和停机时间,从而为制造商节省大量成本。
通过利用从他们的分析中收集到的数据,团队可以通过先进的图形和定量分析技术自信地预测产品寿命和可靠性。通过这样做,他们会在潜在的机械故障发生之前更加安全地了解它们。这些见解将帮助他们评估与设计或目标相关的能源效率低下的风险,并预测优化结果 - 同时快速高效地工作。
最后,我们将介绍我们的第三个能源消耗策略。
策略 3:定期监控您的流程和材料
优化能源效率的另一种方法是定期监控工厂的流程和材料。这允许跨团队进行改进,以查明根本原因并简化整个组织的问题解决。
现实生活中的用例
世界上最大的太阳能技术和可再生能源公司之一在发现其制造过程中存在不一致后,需要控制氮化硅薄膜的厚度。
使用Minitab 和 Minitab Engage™中提供的强大图表和分析工具,该公司能够查明并纠正薄膜厚度差异的原因。
借助 Minitab 强大的分析和改进解决方案,该制造商能够将其面板的能源效率提高7%,并将其年收入增加超过100,000 美元/年。
在对制造过程应用更改之前,已发布产品的质量需要保持一致。Minitab 拥有可确保您的产品质量满足客户期望并符合监管标准的解决方案。
其他需要考虑的例子:
1.如果您希望在投资成本和能源效率之间进行权衡分析,Minitab 中的Graph Builder将是一个很好的解决方案。
2.Minitab Engage 中可用的DMAIC项目可用于跟踪改进,而 Monte Carlo 可用于模拟针对您的计划提出的更改。
结论
这些只是您的组织可以实施以实现节能成功的众多策略中的一小部分。从数据中获得的见解可以帮助您确定最适合您的业务的策略,而 Minitab 是您实现能源效率的端到端分析和 CI 解决方案。 收起阅读 »
选择实验设计中的最优设计
我们知道,DOE在质量控制的整个过程中扮演了非常重要的角色,它是我们产品质量提高,工艺流程改善的重要保证。但基于实验环境和实验成本等因素考虑,有时,我们并不能够实现所有的因子水平组合。这样我们就需要根据实际场景执行最优设计。
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
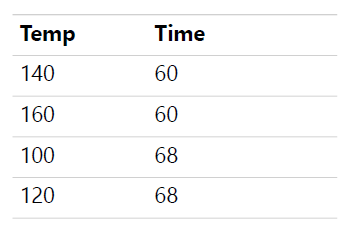
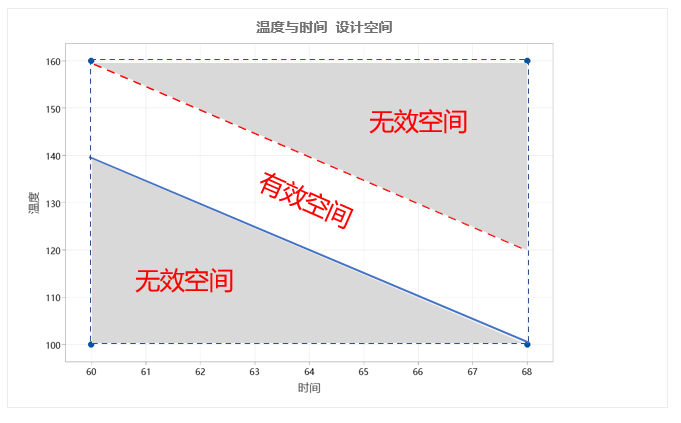
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
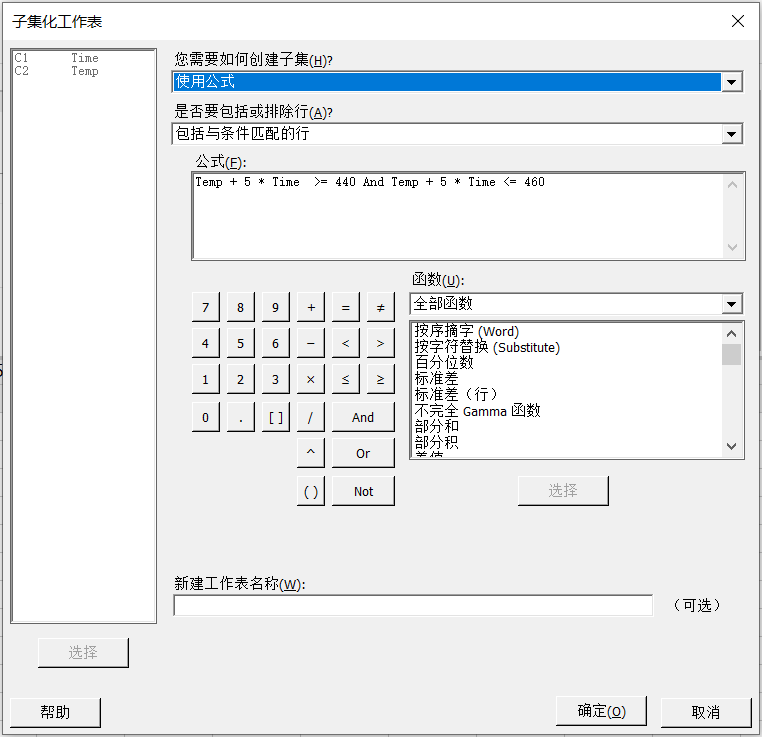
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
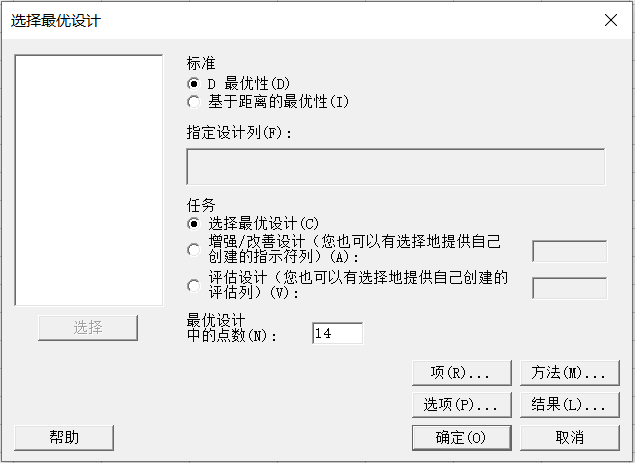
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
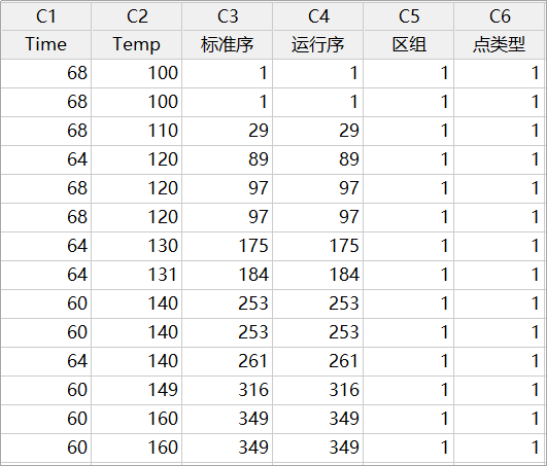
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
收起阅读 »
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
收起阅读 »
验证您的数据是否正常且符合 FDA 要求
Deloitte 专家在其《数据完整性报告 1》中表示,“由高度监管的生命科学公司生成的数据保持完整性至关重要,原因在于,在产品得到审批并随后投放到市场以供人们使用之前,正确记录的信息是制造商确保产品质量、安全性和功效的基础。为了确保患者安全性,数据完整性对于制造过程中的质量控制过程也很重要。”
随着全球监管机构对数据完整性的关注度不断提高,不遵守规定的公司可能会面临从发布公开警告函到接受刑事指控在内的处罚。另外,可能会发生产品从市场中剔除的情况。近年来,数据实践相关问题的数量和类型显著增加,包括未经授权进行数据访问、缺乏已启用的审计跟踪以及意外和蓄意篡改记录。
根据 RAPS 的出版物《监管重点 2》,“在过去三年中,涉及数据完整性问题的警告函数量有所增加,从 2019 财年(财政年度)的 47% 增加到 2020 财年的 51%,再到 2021 财年的 65%”。
美国 FDA 及其欧洲同行提出了与患者安全性相关的要求。在这篇贴文中,我们将重点介绍由 FDA 引入的 ALCOA+ 概念。您将了解 Minitab 解决方案如何帮助巩固可提高数据质量的良好实践,并使公司能够做出以分析和准确数据为后盾的战略性决策。
ALCOA 是“Attributable, Legible, Contemporaneous, Original and Accurate”的缩写,是指数据可追溯、易读、同步、原始和准确
可追溯
您知道谁访问或使用了您的数据吗?
企业需要能够监控谁手动或以电子方式记录和/或处理了数据。
数据源应在其整个生命周期(从收集到研究、分析运行和测试系统)中进行跟踪。
Minitab 的数据集成、自动化、监控和分析报告平台 Minitab Connect 提供审计跟踪功能。审计跟踪可确保跟踪所有在运行时涉及数据的活动:收集、聚合、处理、编译、图形输出、分析报告和控制台。公司始终可以提供有关数据何时何地被访问以及由谁访问的详细信息。
易读
您的数据是否可以随时随地可供访问和读取?
对于所记录的数据,您应该能够永久查看和使用。由于数据是以电子方式存储的,因此数据始终可以在线获取,并通过 Minitab Connect 和 Minitab Statistical Software 内的存储库获取。
同步
在活动发生时是否记录了数据?
在生成和处理过程中都应记录数据。
Minitab Connect 的审计跟踪功能可确保随时准确高效地记录数据。
原始
数据是否经过认证而且真实?
数据应以未更改的原始状态存储。
Minitab Statistical Software 中的命令历史记录可以帮助检索原始数据。数据治理平台 Minitab Connect 跟踪原始数据。
准确
您的数据是否毫无错误?
数据必须反映其真实的实际价值,它应当是真实的。
测量系统分析是统计的一个分支,可以让您快速评估和改进测量系统,从而确保所收集的数据既准确又精确。
如果不对测量系统进行分析,很可能会使数据的变异和不一致性增加,从而对分析造成不利影响。
Minitab Statistical Software 中的测量系统分析 (MSA) 菜单可以帮助您检查操作员和测量设备是否提供准确、一致且精确的信息。
当收集定量数据时,量具重复性与再现性 (R&R) 分析确认仪器和操作员按照一致的方式测量部件。
如果您正在对部件进行评级或者正在识别缺陷,则属性一致性分析会验证不同的评估人员所做的判断是否彼此一致,以及是否符合既定标准。
医药公司和卫生部门下属各组织必须采用更完整、更复杂的技术,这些技术主要用于过程验证、测量不精确和存在偏差等情况。为满足此类要求,执行“关键检查”是不错的做法。 收起阅读 »
随着全球监管机构对数据完整性的关注度不断提高,不遵守规定的公司可能会面临从发布公开警告函到接受刑事指控在内的处罚。另外,可能会发生产品从市场中剔除的情况。近年来,数据实践相关问题的数量和类型显著增加,包括未经授权进行数据访问、缺乏已启用的审计跟踪以及意外和蓄意篡改记录。
根据 RAPS 的出版物《监管重点 2》,“在过去三年中,涉及数据完整性问题的警告函数量有所增加,从 2019 财年(财政年度)的 47% 增加到 2020 财年的 51%,再到 2021 财年的 65%”。
美国 FDA 及其欧洲同行提出了与患者安全性相关的要求。在这篇贴文中,我们将重点介绍由 FDA 引入的 ALCOA+ 概念。您将了解 Minitab 解决方案如何帮助巩固可提高数据质量的良好实践,并使公司能够做出以分析和准确数据为后盾的战略性决策。
ALCOA 是“Attributable, Legible, Contemporaneous, Original and Accurate”的缩写,是指数据可追溯、易读、同步、原始和准确
可追溯
您知道谁访问或使用了您的数据吗?
企业需要能够监控谁手动或以电子方式记录和/或处理了数据。
数据源应在其整个生命周期(从收集到研究、分析运行和测试系统)中进行跟踪。
Minitab 的数据集成、自动化、监控和分析报告平台 Minitab Connect 提供审计跟踪功能。审计跟踪可确保跟踪所有在运行时涉及数据的活动:收集、聚合、处理、编译、图形输出、分析报告和控制台。公司始终可以提供有关数据何时何地被访问以及由谁访问的详细信息。
易读
您的数据是否可以随时随地可供访问和读取?
对于所记录的数据,您应该能够永久查看和使用。由于数据是以电子方式存储的,因此数据始终可以在线获取,并通过 Minitab Connect 和 Minitab Statistical Software 内的存储库获取。
同步
在活动发生时是否记录了数据?
在生成和处理过程中都应记录数据。
Minitab Connect 的审计跟踪功能可确保随时准确高效地记录数据。
原始
数据是否经过认证而且真实?
数据应以未更改的原始状态存储。
Minitab Statistical Software 中的命令历史记录可以帮助检索原始数据。数据治理平台 Minitab Connect 跟踪原始数据。
准确
您的数据是否毫无错误?
数据必须反映其真实的实际价值,它应当是真实的。
测量系统分析是统计的一个分支,可以让您快速评估和改进测量系统,从而确保所收集的数据既准确又精确。
如果不对测量系统进行分析,很可能会使数据的变异和不一致性增加,从而对分析造成不利影响。
Minitab Statistical Software 中的测量系统分析 (MSA) 菜单可以帮助您检查操作员和测量设备是否提供准确、一致且精确的信息。
当收集定量数据时,量具重复性与再现性 (R&R) 分析确认仪器和操作员按照一致的方式测量部件。
如果您正在对部件进行评级或者正在识别缺陷,则属性一致性分析会验证不同的评估人员所做的判断是否彼此一致,以及是否符合既定标准。
医药公司和卫生部门下属各组织必须采用更完整、更复杂的技术,这些技术主要用于过程验证、测量不精确和存在偏差等情况。为满足此类要求,执行“关键检查”是不错的做法。 收起阅读 »
价值流图降低供应链成本的8种方式
价值流图(VSM)是一个强大的工具,可以用来优化供应链中的物流和信息流。通过分析和可视化从原材料到成品的整个过程,组织可以确定瓶颈、低效和需要改进的地方。一旦确定了这些问题,组织就可以实施变革,以改善供应链中的材料和信息流,最终降低成本,提高利润。以下是价值流图帮助降低供应链成本的8种方式:
1.降低库存成本
通过识别和消除生产过程中的浪费,公司可以减少需要持有的库存量,从而节省存储、保险和处理成本。这也可以节省资本成本,因为库存中的资金减少了。
2.缩短交货时间
通过识别生产过程中的瓶颈和延迟,公司可以缩短向客户交付产品的交付时间,从而节省运输成本并提高客户满意度。这还可以降低催货和空运的成本,并提高准时交付的绩效。
3.提高效率
通过消除生产过程中的浪费和低效,公司可以减少能源消耗,最大限度地减少废料和返工,并提高机器利用率。
4.减少废料和返工
通过识别和消除缺陷的原因,公司可以减少因生产过剩或缺乏质量控制而产生的废品和返工。
5.减少停机时间
通过识别和消除瓶颈和延迟,公司可以减少因生产过剩或资源不足而导致的停机时间,从而通过提高生产率和降低维护成本来节约成本。
6.提高客户满意度
通过缩短交付周期、增加准时交付和提高产品质量,公司可以提高客户满意度,从而通过减少退货、增加销售和提高客户忠诚度来节约成本。
7.改善供应商关系
通过识别供应商的问题,如交货时间的延迟,组织可以采取措施改善这些关系,并协商更好的价格或交货条款。这有助于降低原材料和其他资源的成本。
8.降低运营成本
通过分析整个供应链流程,价值流图可以帮助确定可以降低成本的领域,例如减少供应商数量、整合订单或减少包装材料。
使用正确的工具
价值流图当然可以在纸上完成,使用强大的可视化业务工具,如Minitab工作空间或者迷你标签接合可以使这一过程变得容易得多,尤其是当您的团队位于不同的地区或办公地点时。
收起阅读 »
1.降低库存成本
通过识别和消除生产过程中的浪费,公司可以减少需要持有的库存量,从而节省存储、保险和处理成本。这也可以节省资本成本,因为库存中的资金减少了。
2.缩短交货时间
通过识别生产过程中的瓶颈和延迟,公司可以缩短向客户交付产品的交付时间,从而节省运输成本并提高客户满意度。这还可以降低催货和空运的成本,并提高准时交付的绩效。
3.提高效率
通过消除生产过程中的浪费和低效,公司可以减少能源消耗,最大限度地减少废料和返工,并提高机器利用率。
4.减少废料和返工
通过识别和消除缺陷的原因,公司可以减少因生产过剩或缺乏质量控制而产生的废品和返工。
5.减少停机时间
通过识别和消除瓶颈和延迟,公司可以减少因生产过剩或资源不足而导致的停机时间,从而通过提高生产率和降低维护成本来节约成本。
6.提高客户满意度
通过缩短交付周期、增加准时交付和提高产品质量,公司可以提高客户满意度,从而通过减少退货、增加销售和提高客户忠诚度来节约成本。
7.改善供应商关系
通过识别供应商的问题,如交货时间的延迟,组织可以采取措施改善这些关系,并协商更好的价格或交货条款。这有助于降低原材料和其他资源的成本。
8.降低运营成本
通过分析整个供应链流程,价值流图可以帮助确定可以降低成本的领域,例如减少供应商数量、整合订单或减少包装材料。
使用正确的工具
价值流图当然可以在纸上完成,使用强大的可视化业务工具,如Minitab工作空间或者迷你标签接合可以使这一过程变得容易得多,尤其是当您的团队位于不同的地区或办公地点时。
收起阅读 »
预测分析:帮助规划 DOE 的完美合作伙伴
实验设计有显着的好处。它们可用于多种情况,并有效地允许操纵多个输入因素以确定它们对所需响应的影响。他们还确定了在一次试验一个因素时可能会遗漏的重要交互作用。
DOE 的规划阶段对于成功至关重要。由于在规划阶段发现的障碍,DOE 经常停滞不前。例如,看起来过于昂贵或复杂或缺乏关键信息的 DOE 通常在它们有机会执行之前就被废弃了。幸运的是,先进的预测分析 是一个强大的工具,可以帮助消除创建 DOE 的障碍,甚至可以提高成功的机会。
问题 1:您想运行筛选设计,但您不能停止系统(或进程)运行以收集数据或收集数据非常昂贵。
从业者使用筛选实验设计(筛选 DOE)从许多潜在变量的领域中识别过程中最重要的变量。它们使从业者能够减少实验的规模,从而节省时间和金钱。如果数据难以获取或成本高昂,则尤其如此。
当您无法停止系统或进程来运行筛选实验时会发生什么?或者,如果收集用于筛选的数据点非常昂贵,以至于难以证明这样做是合理的?
解决方案 1:预测分析可以帮助您轻松识别最重要的变量。
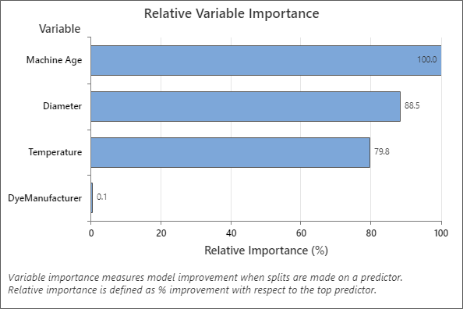
不要害怕,预测分析就在这里!通过分析来自您的系统或流程的数据,您可以利用您最喜欢的机器学习算法或运行自动化机器学习来识别对您的响应有潜在影响的预测因素。Minitab 通过我们专为帮助您识别最重要的变量而构建的相对变量重要性图表使这一过程变得简单。查看我们的网络研讨会 DOE 实践,链接如下示例。
问题 2:您想运行设计实验,但对因素(即水平)的适当范围(即上限和下限)不确定。
运行 DOE 时,实验在不同的因子值(称为水平)下运行。这些水平是我们衡量响应的自变量,我们传统上将其称为因变量。例如,如果您尝试优化一台设备的速度,则需要设置最高和最低速度的限制以构建速度范围以优化您的过程。另一个例子可能是烘烤蛋糕时烤箱的温度。根据您的经验,您可能知道低于 300F 不会烘烤蛋糕,而在 400F 时会烧焦,因此您可以设置限制。但是,如果您以前从未烤过蛋糕怎么办?或者,如果您有一台新机器而不知道在哪里设置限制怎么办?
解决方案 2:预测分析提供可视化效果来帮助您设置合理的限制。
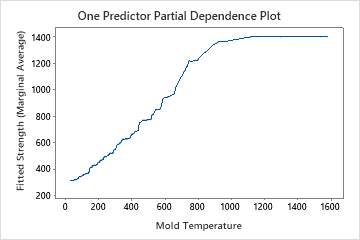
当您运行 Minitab 的预测分析时,您将生成可视化效果,展示一个或多个变量对预测结果的影响。为了预测结果,这些图的目的是突出响应和变量之间的关系是线性的、单调的还是更复杂的。这些可视化对于 DOE 也非常有用。
在上面的示例中,假设您正在尝试运行优化强度的实验。您可能了解模具温度与强度之间的关系,但也知道简单地将机器调到最高温度可能会产生不利影响,例如过热或不必要地增加生产成本。您还知道实验中可能会与其他变量(例如压力)发生相互作用。通过查看图表,您会发现温度高于 1200 会导致强度边际增加。对于您设计的实验,您可以将模具温度水平设置为 1000 和 1200,以运行以最大化强度为目标的实验。但是,如果目标是最小化强度,您可以从图中看出,在较低的模具温度范围内进行测试会更合理。
预测分析只是与 DOE 携手并进的众多工具之一。
DOE 是许多从业者的重要工具,不应孤立存在。如前所述,规划对于 DOE 的成功至关重要,这就是 Minitab 创建专门为帮助规划过程而构建的DOE 规划工作表的原因。如果您是 DOE 的新手或只是想提高您的技能组合,Minitab 会提供支持、资源和解决方案来帮助您前进。 收起阅读 »
DOE 的规划阶段对于成功至关重要。由于在规划阶段发现的障碍,DOE 经常停滞不前。例如,看起来过于昂贵或复杂或缺乏关键信息的 DOE 通常在它们有机会执行之前就被废弃了。幸运的是,先进的预测分析 是一个强大的工具,可以帮助消除创建 DOE 的障碍,甚至可以提高成功的机会。
问题 1:您想运行筛选设计,但您不能停止系统(或进程)运行以收集数据或收集数据非常昂贵。
从业者使用筛选实验设计(筛选 DOE)从许多潜在变量的领域中识别过程中最重要的变量。它们使从业者能够减少实验的规模,从而节省时间和金钱。如果数据难以获取或成本高昂,则尤其如此。
当您无法停止系统或进程来运行筛选实验时会发生什么?或者,如果收集用于筛选的数据点非常昂贵,以至于难以证明这样做是合理的?
解决方案 1:预测分析可以帮助您轻松识别最重要的变量。
不要害怕,预测分析就在这里!通过分析来自您的系统或流程的数据,您可以利用您最喜欢的机器学习算法或运行自动化机器学习来识别对您的响应有潜在影响的预测因素。Minitab 通过我们专为帮助您识别最重要的变量而构建的相对变量重要性图表使这一过程变得简单。查看我们的网络研讨会 DOE 实践,链接如下示例。
问题 2:您想运行设计实验,但对因素(即水平)的适当范围(即上限和下限)不确定。
运行 DOE 时,实验在不同的因子值(称为水平)下运行。这些水平是我们衡量响应的自变量,我们传统上将其称为因变量。例如,如果您尝试优化一台设备的速度,则需要设置最高和最低速度的限制以构建速度范围以优化您的过程。另一个例子可能是烘烤蛋糕时烤箱的温度。根据您的经验,您可能知道低于 300F 不会烘烤蛋糕,而在 400F 时会烧焦,因此您可以设置限制。但是,如果您以前从未烤过蛋糕怎么办?或者,如果您有一台新机器而不知道在哪里设置限制怎么办?
解决方案 2:预测分析提供可视化效果来帮助您设置合理的限制。
当您运行 Minitab 的预测分析时,您将生成可视化效果,展示一个或多个变量对预测结果的影响。为了预测结果,这些图的目的是突出响应和变量之间的关系是线性的、单调的还是更复杂的。这些可视化对于 DOE 也非常有用。
在上面的示例中,假设您正在尝试运行优化强度的实验。您可能了解模具温度与强度之间的关系,但也知道简单地将机器调到最高温度可能会产生不利影响,例如过热或不必要地增加生产成本。您还知道实验中可能会与其他变量(例如压力)发生相互作用。通过查看图表,您会发现温度高于 1200 会导致强度边际增加。对于您设计的实验,您可以将模具温度水平设置为 1000 和 1200,以运行以最大化强度为目标的实验。但是,如果目标是最小化强度,您可以从图中看出,在较低的模具温度范围内进行测试会更合理。
预测分析只是与 DOE 携手并进的众多工具之一。
DOE 是许多从业者的重要工具,不应孤立存在。如前所述,规划对于 DOE 的成功至关重要,这就是 Minitab 创建专门为帮助规划过程而构建的DOE 规划工作表的原因。如果您是 DOE 的新手或只是想提高您的技能组合,Minitab 会提供支持、资源和解决方案来帮助您前进。 收起阅读 »
在 Minitab 中更轻松地可视化数据中的变异性:查看变异性图表
良好的数据分析可以让您更快地做出更明智的决策。在 Minitab,我们一直在努力让您更轻松地分析数据和传达这些结果,以便您可以继续推进您的项目。恰当的例子:Minitab 中的变异图。
可变性图表可以轻松识别数据中的可变性来源;无论您是将其用作初步分析工具还是在最终报告中用于证明主要变异来源。
示例 1:交流临床研究的结果
考虑一项临床研究,食品制造商调查了六种产品的风味差异。研究在第 2 天重复进行。以下示例显示了数据的排列方式:
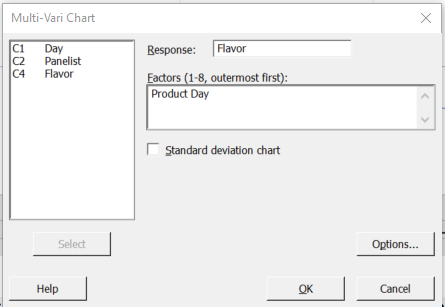
我们首先选择Stat > Quality Tools > Variability Chart 下的 Variability Chart …
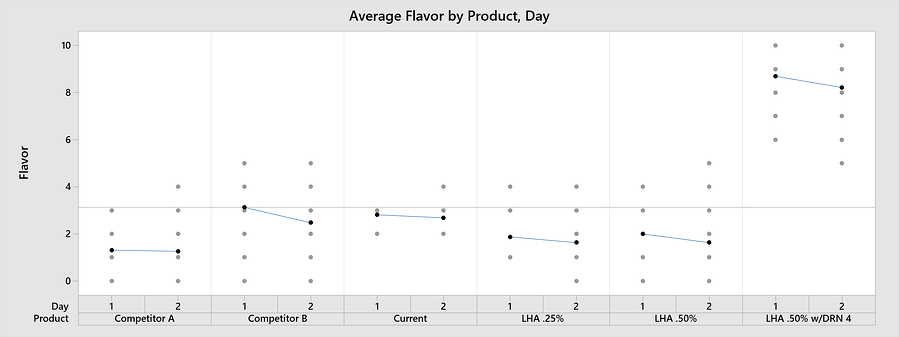
纵轴代表风味评分,横轴包含产品代码和天数。
很容易看出,LHA .50% w/ DRN 4产品在这两天的平均风味评分(由线条连接)更高。此外,通过变异性图表可以很容易地看出,与所有其他产品相比,当前产品的风味评分差异要小得多。
如果目标是最大化风味,一个合理的结论是,虽然当前产品提供更一致的风味,但LHA .50% w/ DRN 4产品将需要一些工作来减少这些风味评分的变化。变异性图表是展示本研究结果的绝佳选择,因为它以清晰、简洁的视图显示了LHA .50% w/ DRN 4产品的较高平均分数和当前产品的少量变异。
示例 2:可视化从医疗设备制造过程中收集的数据
现在考虑我们已经从测量医用泵输液量的过程中收集了数据。我们使用两种不同的材料类型在两条输送线上以四种不同的泵速收集数据。这是一个显示数据排列方式的示例:
与第一个示例一样,我们在Stat > Quality Tools > Variability Chart中找到了 Variability Chart 对话框……在这里我们还选择了Standard deviation chart:
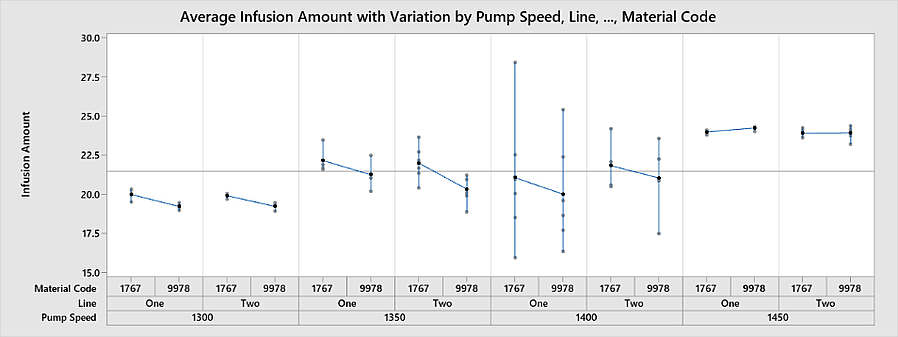
使用变异图可以很容易地将这三个因素可视化在一个图表中:
我们可以看到总体平均值约为21.5,用水平线表示所有级别。泵速1300内的可变性表明结果低于总体平均值。我们还可以看到材料代码 9978在第一行和第二行的灌注测量值始终较低。还很容易看出,与其他泵速相比, Pump Speed 1400内的可变性要高得多。
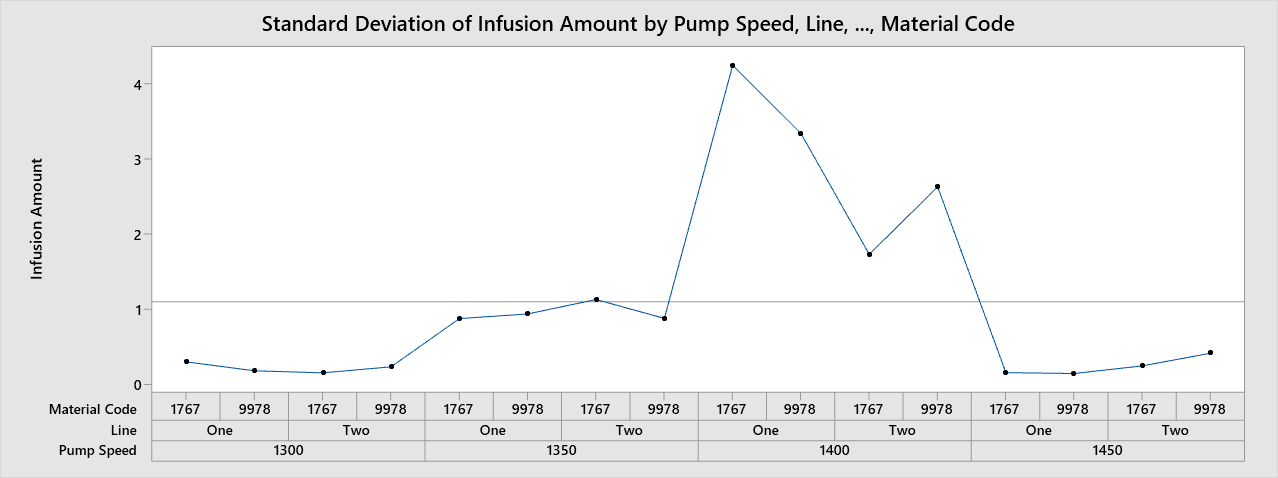
Variability Chart 还提供了一个选项来创建数据的标准偏差图 - 在这里很容易看到泵速为1400时的变化在Line和Material Code的水平上更高。
收起阅读 »
可变性图表可以轻松识别数据中的可变性来源;无论您是将其用作初步分析工具还是在最终报告中用于证明主要变异来源。
示例 1:交流临床研究的结果
考虑一项临床研究,食品制造商调查了六种产品的风味差异。研究在第 2 天重复进行。以下示例显示了数据的排列方式:
我们首先选择Stat > Quality Tools > Variability Chart 下的 Variability Chart …
纵轴代表风味评分,横轴包含产品代码和天数。
很容易看出,LHA .50% w/ DRN 4产品在这两天的平均风味评分(由线条连接)更高。此外,通过变异性图表可以很容易地看出,与所有其他产品相比,当前产品的风味评分差异要小得多。
如果目标是最大化风味,一个合理的结论是,虽然当前产品提供更一致的风味,但LHA .50% w/ DRN 4产品将需要一些工作来减少这些风味评分的变化。变异性图表是展示本研究结果的绝佳选择,因为它以清晰、简洁的视图显示了LHA .50% w/ DRN 4产品的较高平均分数和当前产品的少量变异。
示例 2:可视化从医疗设备制造过程中收集的数据
现在考虑我们已经从测量医用泵输液量的过程中收集了数据。我们使用两种不同的材料类型在两条输送线上以四种不同的泵速收集数据。这是一个显示数据排列方式的示例:
与第一个示例一样,我们在Stat > Quality Tools > Variability Chart中找到了 Variability Chart 对话框……在这里我们还选择了Standard deviation chart:
使用变异图可以很容易地将这三个因素可视化在一个图表中:
我们可以看到总体平均值约为21.5,用水平线表示所有级别。泵速1300内的可变性表明结果低于总体平均值。我们还可以看到材料代码 9978在第一行和第二行的灌注测量值始终较低。还很容易看出,与其他泵速相比, Pump Speed 1400内的可变性要高得多。
Variability Chart 还提供了一个选项来创建数据的标准偏差图 - 在这里很容易看到泵速为1400时的变化在Line和Material Code的水平上更高。
收起阅读 »
什么时候适合使用逐步回归?
我发现了一个很有意思的例子,是关于识别某制造厂的主要能源使用来源。
什么时候适合使用逐步回归?
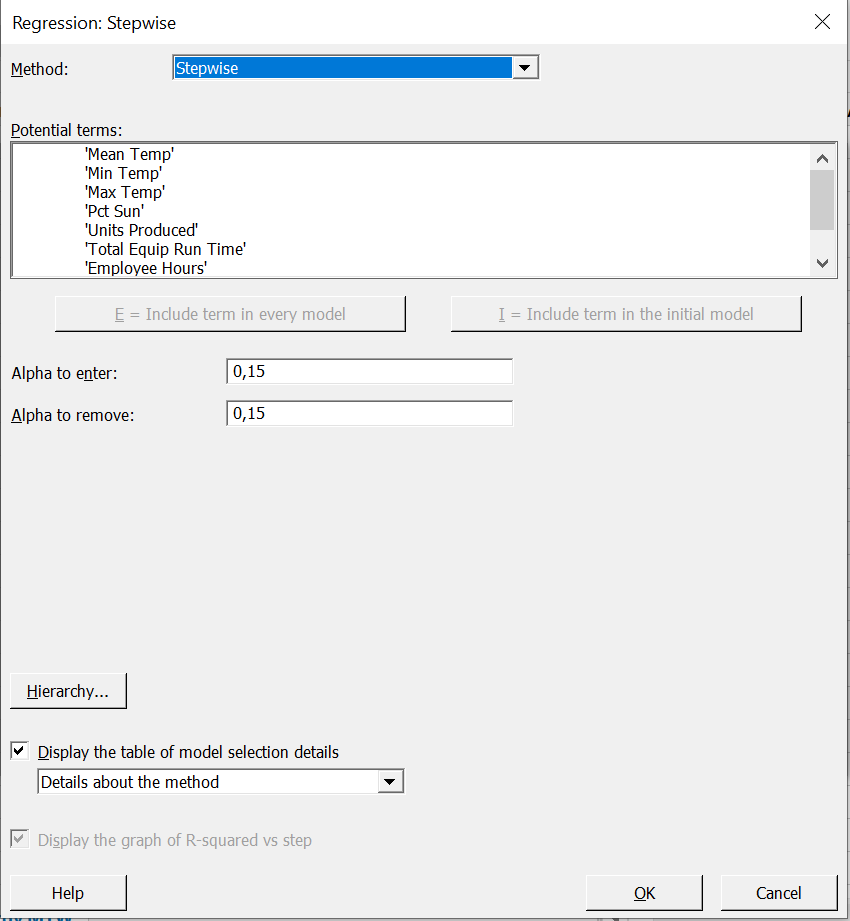
当您有许多变量并且想确认有用的预测变量子集时,逐步回归就是一种合适的分析方法。在 Minitab 中,标准的逐步回归程序每次都只添加和删除一个预测变量。当模型中未包含的所有变量的 p 值都大于指定的入选用 Alpha 值,且模型中所有变量的 p 值都小于或等于指定的删除用 Alpha 值时,Minitab 停止。除了标准逐步法外,Minitab 还提供另两种逐步程序:
* 向前选择法: Minitab 以模型中没有任何预测变量开始,并为每个步骤添加最显著的变量。当模型中未包含的所有变量的 p 值都大于指定的入选用 Alpha 值,Minitab 将停止。
* 向后消元法: Minitab 以模型中包含所有预测变量开始,并删除每个步骤的最小显著项。当模型中包含的所有变量的 p 值都小于或等于指定的删除用 Alpha 值时,Minitab 将停止。
逐步回归示例
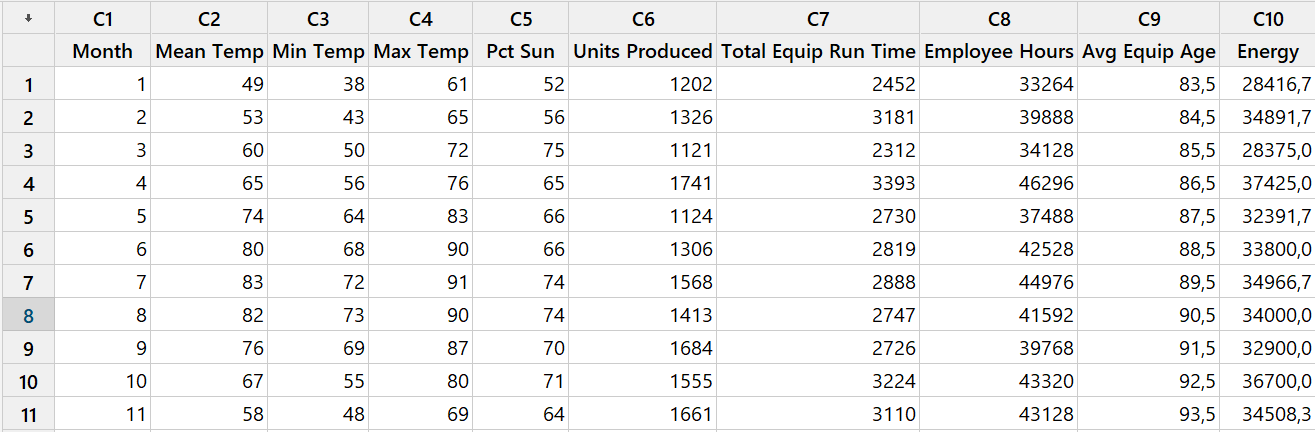
本示例使用逐步回归识别主要的能源使用来源。制造厂的分析师考虑了以下预测变量:生产产品总数、设备总运行时间、员工人数、平均室外温度、最低室外温度、最高室外温度、日照百分率以及设备平均寿命。但值得注意的是,当预测变量达到 100 个以上时,逐步回归会非常有用!
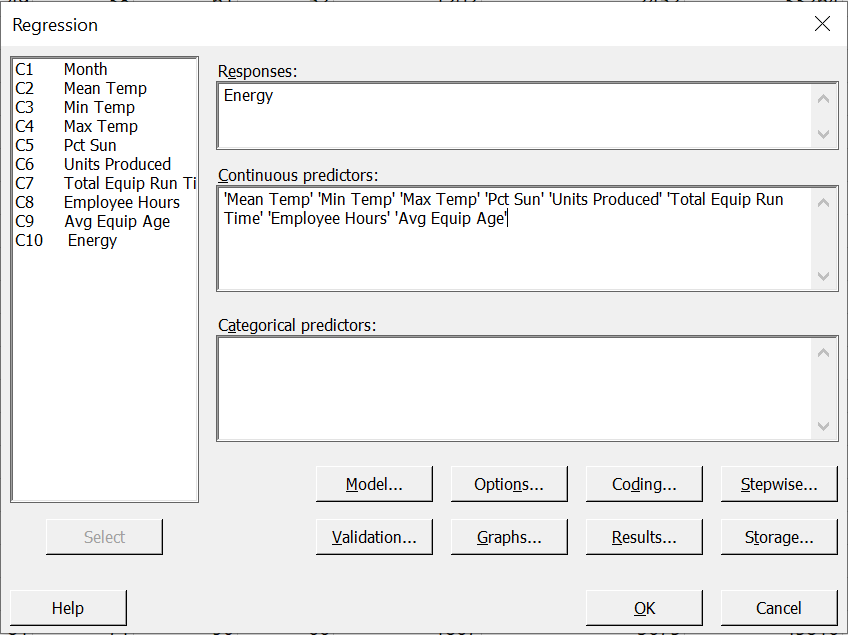
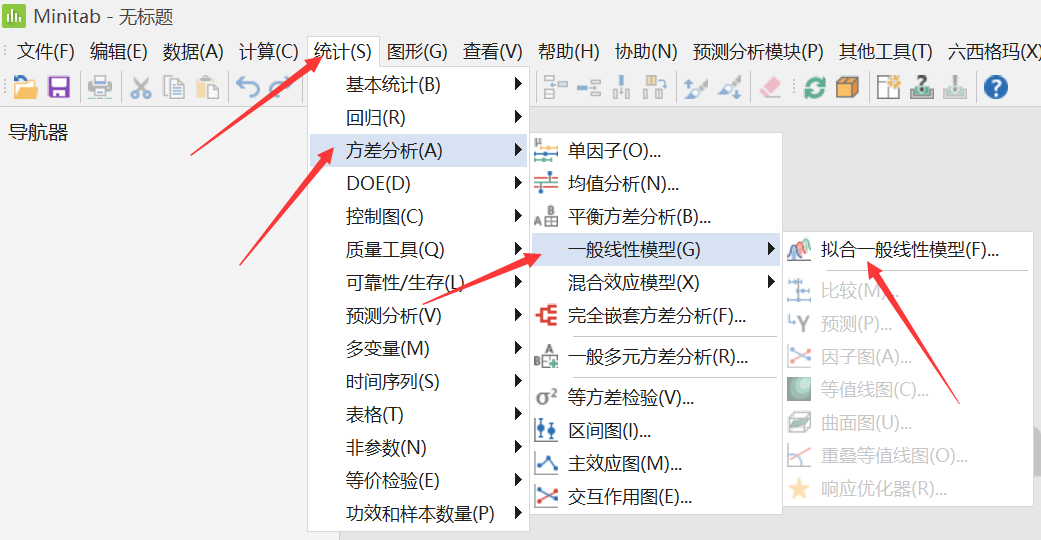
他们的目的是将这些变量缩小到能源使用的主要预测变量列表中。为得到最终模型,在 Minitab 中选择统计 > 回归 > 逐步,并输入响应“能源”和上面的预测变量列表来完成对话框。
他们的目的是将这些变量缩小到能源使用的主要预测变量列表中。为得到最终模型,在 Minitab 中选择统计 > 回归 > 逐步,并输入响应“能源”和上面的预测变量列表来完成对话框。
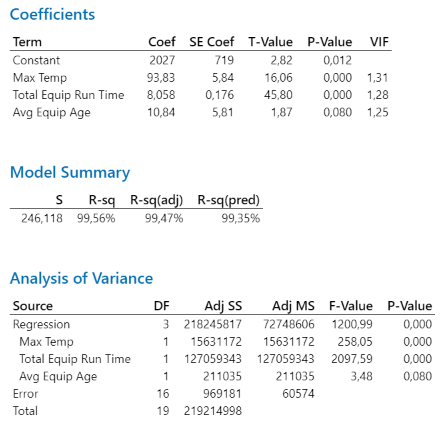
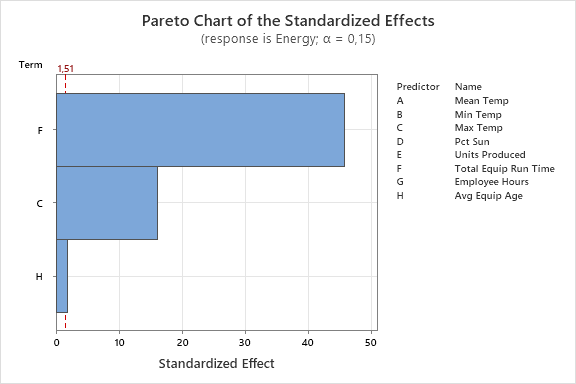
他们得到了下面的模型,该模型中包含了设备总运行时间、最高温度和设备平均寿命三个预测变量。Minitab 删除了其他变量,因为这些变量的 p 值大于入选用 Alpha 值。
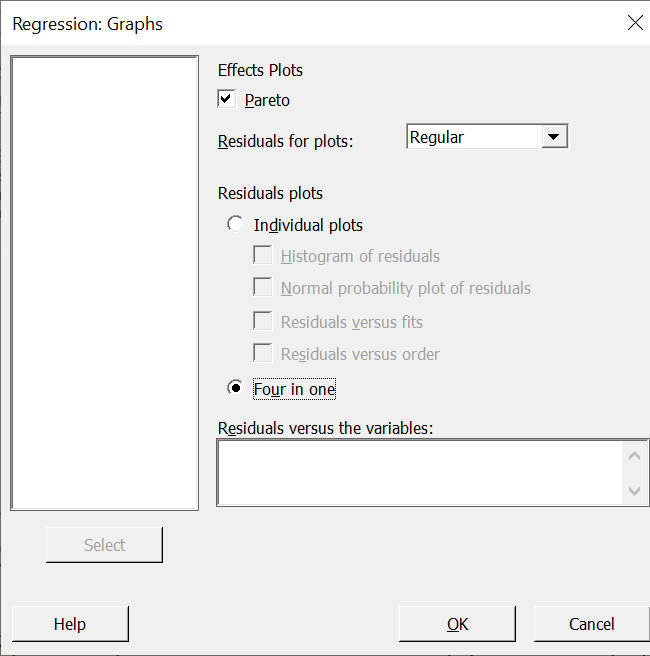
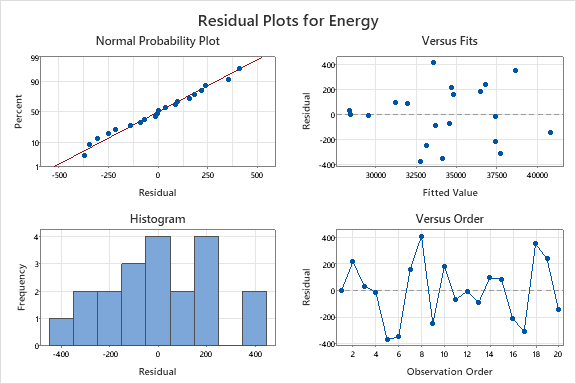
为获得最终模型,分析师选择统计 > 回归 > 回归,并通过将“能源”作为响应,且三个显著变量作为预测变量来完成对话框。(要检查残差图,在对话框中选择图形,然后在残差图下,选择四合一。)
以下回归方程表明,随着设备总运行时间、最高温度和设备平均寿命的增加,能源使用也相应增加:
根据 T 统计值,设备总运行时间的影响最大,最高温度次之,然后是设备平均寿命。
通过分析,分析师可以得出这样的结论:由于大量使用空调,能源使用显著增高;而较新的设备看上去降低了能源使用。工厂可能想要在持续使用空调的高峰期限制设备的运行,并考虑在夏季来临前购置新设备。
P逐步回归的陷阱
虽然逐步回归能帮助我们了解很多,但也存在一些需要注意的潜在陷阱:
· 如果两个独立变量高度相关,那么即使他们都很重要,模型中可能只包含其中一个。
· 由于该程序可以拟合许多模型,因此可能只是偶然的选择了恰好拟合数据的模型。
· 对于给定数量的预测变量,逐步回归可能不会总是以具有最高 R2 值的模型结束。
· 自动程序无法考虑分析师可能掌握对数据的特殊知识。因此,所选的模型可能不是最实用的。
· 根据响应来绘制单个预测变量图通常具有误导性,因为图形没有考虑模型中的其他预测变量。 收起阅读 »
什么时候适合使用逐步回归?
当您有许多变量并且想确认有用的预测变量子集时,逐步回归就是一种合适的分析方法。在 Minitab 中,标准的逐步回归程序每次都只添加和删除一个预测变量。当模型中未包含的所有变量的 p 值都大于指定的入选用 Alpha 值,且模型中所有变量的 p 值都小于或等于指定的删除用 Alpha 值时,Minitab 停止。除了标准逐步法外,Minitab 还提供另两种逐步程序:
* 向前选择法: Minitab 以模型中没有任何预测变量开始,并为每个步骤添加最显著的变量。当模型中未包含的所有变量的 p 值都大于指定的入选用 Alpha 值,Minitab 将停止。
* 向后消元法: Minitab 以模型中包含所有预测变量开始,并删除每个步骤的最小显著项。当模型中包含的所有变量的 p 值都小于或等于指定的删除用 Alpha 值时,Minitab 将停止。
逐步回归示例
本示例使用逐步回归识别主要的能源使用来源。制造厂的分析师考虑了以下预测变量:生产产品总数、设备总运行时间、员工人数、平均室外温度、最低室外温度、最高室外温度、日照百分率以及设备平均寿命。但值得注意的是,当预测变量达到 100 个以上时,逐步回归会非常有用!
他们的目的是将这些变量缩小到能源使用的主要预测变量列表中。为得到最终模型,在 Minitab 中选择统计 > 回归 > 逐步,并输入响应“能源”和上面的预测变量列表来完成对话框。
他们的目的是将这些变量缩小到能源使用的主要预测变量列表中。为得到最终模型,在 Minitab 中选择统计 > 回归 > 逐步,并输入响应“能源”和上面的预测变量列表来完成对话框。
他们得到了下面的模型,该模型中包含了设备总运行时间、最高温度和设备平均寿命三个预测变量。Minitab 删除了其他变量,因为这些变量的 p 值大于入选用 Alpha 值。
为获得最终模型,分析师选择统计 > 回归 > 回归,并通过将“能源”作为响应,且三个显著变量作为预测变量来完成对话框。(要检查残差图,在对话框中选择图形,然后在残差图下,选择四合一。)
以下回归方程表明,随着设备总运行时间、最高温度和设备平均寿命的增加,能源使用也相应增加:
根据 T 统计值,设备总运行时间的影响最大,最高温度次之,然后是设备平均寿命。
通过分析,分析师可以得出这样的结论:由于大量使用空调,能源使用显著增高;而较新的设备看上去降低了能源使用。工厂可能想要在持续使用空调的高峰期限制设备的运行,并考虑在夏季来临前购置新设备。
P逐步回归的陷阱
虽然逐步回归能帮助我们了解很多,但也存在一些需要注意的潜在陷阱:
· 如果两个独立变量高度相关,那么即使他们都很重要,模型中可能只包含其中一个。
· 由于该程序可以拟合许多模型,因此可能只是偶然的选择了恰好拟合数据的模型。
· 对于给定数量的预测变量,逐步回归可能不会总是以具有最高 R2 值的模型结束。
· 自动程序无法考虑分析师可能掌握对数据的特殊知识。因此,所选的模型可能不是最实用的。
· 根据响应来绘制单个预测变量图通常具有误导性,因为图形没有考虑模型中的其他预测变量。 收起阅读 »
如何使结晶颗粒大小均等?
Tate & Lyle 是食品与饮料行业的全球领导者,他们的口号是“生产优质食品”,在以下领域有着令人惊叹的辉煌成就:将玉米、木薯淀粉和其他原料制作成配料,以改进食品的口感、质地和营养。该公司在美国最知名的产品之一是甜味剂 SPLENDA® 三氯蔗糖。
当 Tate & Lyle 面临玉米葡萄糖精制过程的挑战时,该公司选择 Minitab 软件来解决问题。
挑战:使结晶颗粒大小均等
在 Adam Russell 最初担任 Tate & Lyle 全球运营黑带大师时,他面临着以下挑战:使他们生产的玉米葡萄糖的颗粒保持同等大小。
“结晶过程的质量特征的一项关键因素就是颗粒大小分布”,Russell 表示,“这究竟为何如此重要?20-30 年前,我们产品的目标客户所期待的是玉米葡萄糖的口感和质地能接近普通的食用糖或蔗糖。为此,我们必须确保颗粒大小分布在一定范围内”。
Tate & Lyle 所面临的难题是,一些颗粒的大小在可接受范围之外,而他们无法找到原因。该公司罗列了一些他们认为对颗粒大小变异造成影响的传统因素:
温度
压力
流速
pH
传导性
相关因素还在不断增加。
Minitab 如何帮助他们
Tate & Lyle 在 Companion by Minitab(现为 Minitab Engage®)中创建的过程图简化版本。在玉米葡萄糖结晶过程中,糖浆由精炼厂提供,然后进行结晶(需要数天完成),接着用离心机进行分离,脱水并装袋,销售给客户。
为解决问题,该公司第一步使用 Companion by Minitab (现为 Minitab Engage®)创建了过程图,详细体现了结晶过程(详细了解过程图)。颗粒大小分布不能可靠地控制在严格范围之内,因此他们想要了解造成变异的原因以及如何进行控制。
“所有项都在一家化工厂内进行测量”,Russell 说道,“每个可能的点都拥有发送器,可为数据历史功能提供信息。这本身非常棒,但也为我们带来了难题,信息量太大,我根本无从着手”。
为了直观地了解颗粒大小数据,Russell 和他的团队使用 Minitab Statistical Software 创建了如下 Xbar chart 控制图.
虽然这些变量之间的多种关系都是非线性的,但是这也证实要发现它们相互之间的影响是非常困难的。此外,颗粒大小在它装袋销售给客户之前是未知的,因为在这之前它处于干燥阶段,其形态是介于液体和固体之间的凝胶状,称为“浆体”。
此类模型具有 1,000 多个可能的输入。多个单独的回归模型并不能寻找到答案。
关键过程指标是制成品的变异系数 (CV),在此显示在使用 Minitab Statistical Software 创建的 Xbar 控制图中。
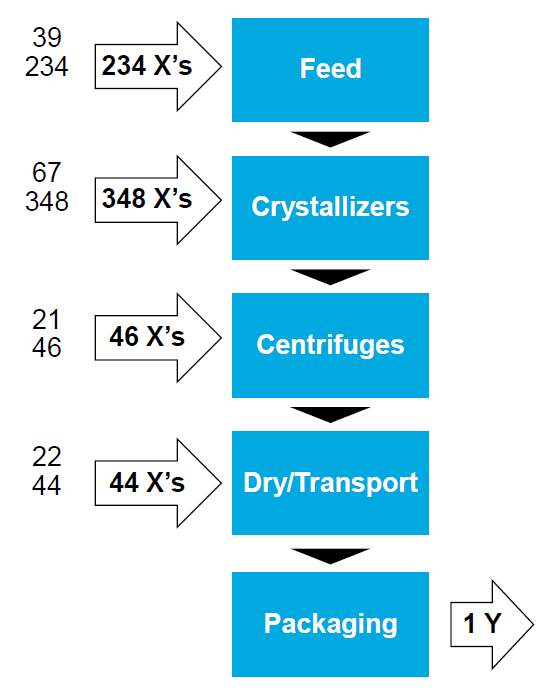
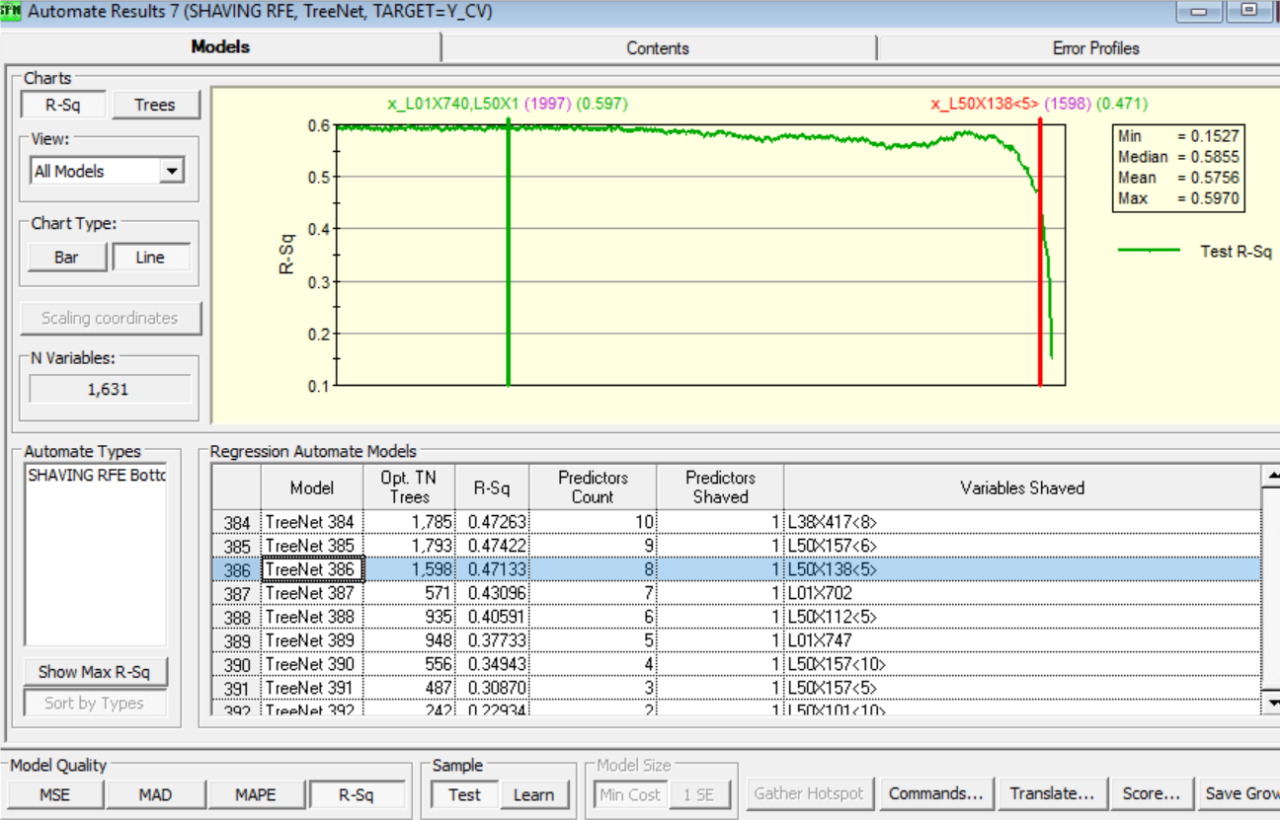
由于多个预测变量以极其复杂的方式相互影响,因此需要采用有组织的方法来标识哪些预测变量对颗粒大小分布的影响最大。他们需要使用 TreeNet 中的 Salford Predictive Modeler (SPM).
“只使用传统建模技术的话,非常困难”,Russell 表示,“我们很难了解变量与结果之间的关系。幸运的是,SPM 的 TreeNet 使我们可以轻松地专注于关键预测变量,并使我们能够设计出能够有效处理这些预测变量的策略。我坚信 Minitab 和 SPM 的 TreeNet 算法可以有效地进行协作。当然,SPM 不能替代 Minitab 或其他统计程序,但当我们将两者结合使用时,我认为我们能更快获得答案,这再好不过了”。
Russell 使用了 TreeNet 中的默认设置并调整了树的数量。当他着手剃除预测变量时,他开始了解它对检验 R 平方值的影响。
此颗粒大小控制模型仅有 8 个预测变量,但能说明检验样本中一半的变异。
为了找出这些关键变量背后真正的含义,Russell 使用了 SPM 的部分依赖图。某些变量落在了部分依赖曲线的陡峭位置,这揭示了它们的重要性。如果不使用 SPM 部分依赖曲线,那么可能无法发现这些变量的重要性。
然后,Russell 使用了一种直接的逐步方法。他每次从中剔除一个变量,然后观察对 R 平方产生的影响。起初并无任何重大改变,直到他剔除第四个最重要的变量。他将此变量告知制造团队并向他们了解此变量的更多信息。
成果
Russell 使用 SPM 的变量重要性排名功能将 1,000 多个预测变量迅速缩减到区区 8 个。而且单这 8 个预测变量就导致了检验样本中的近一半变异。
使用 SPM 的“从顶部剔除”功能,Russell 得以快速分辨出相较于其他任何变量而言对 R 平方的影响更显著的变量。最终证实此变量与结晶系统的原料流相关,但其对最终产品的影响在 Russell 创建 SPM 模型之前并不清晰。
之后,在 SPM 部分依赖图的帮助下,Russell 了解到了此变量对于颗粒大小不可靠性的影响很大。SPM 的部分依赖图展示了在“沿着分布曲线进行”更改时,此变量如何发生改变来响应这些更改。
“我们沿着此分布曲线的陡峭部分进行”,Russell 说道,“幸运的时候,变异系数会较低,而不那么幸运时,变异系数会较高。如果不使用 SPM,我永远也不会了解到这点”。
Russell 实现了他的目标,十分满意,他找到了几种方式来减小玉米葡萄糖晶体最终大小的变异,帮助食品制造商使用这些配料来改进销售给客户的产品。*该案例研究是在 2021 年推出 Minitab Engage 之前使用 Companion by Minitab 创建的。 收起阅读 »
初识变异源分析
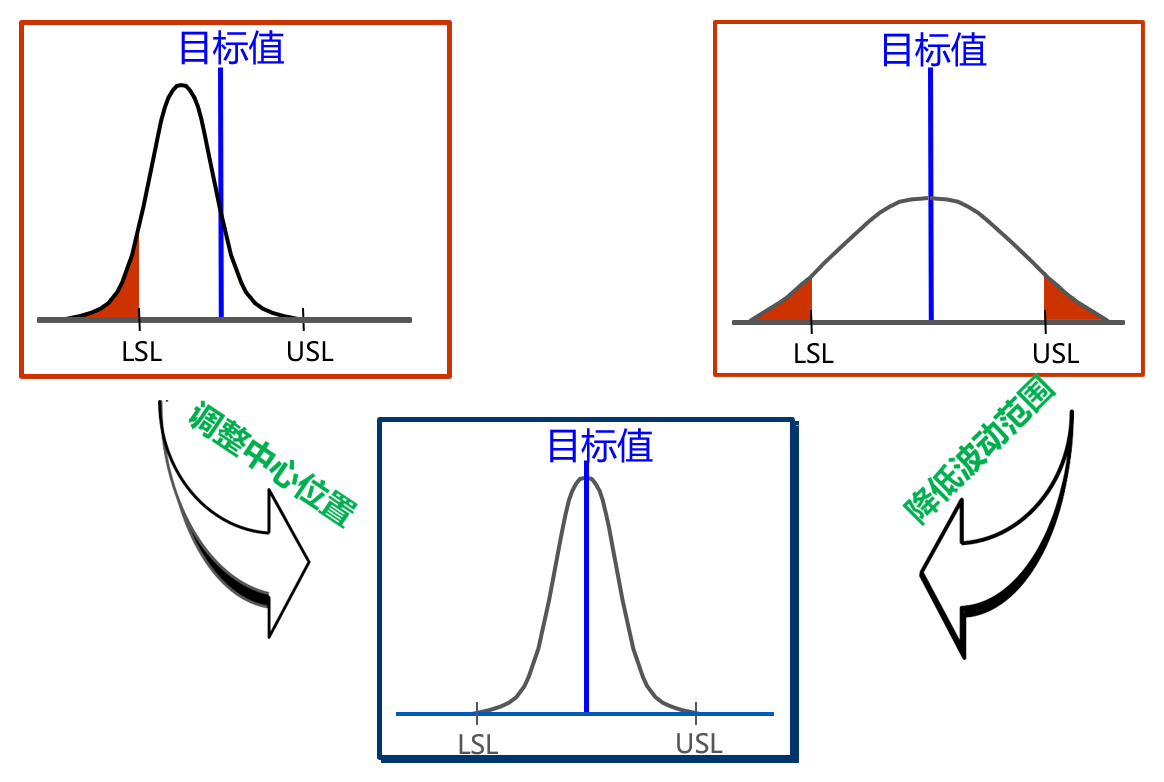
实施六西格玛管理的目标就是希望生产出的产品的特性指标的标准差要尽可能小(只调节均值对中效果有限)。
让标准差尽可能小不是件简单的事,它可能牵涉生产中的很多因素。生产中产生的变异这么大,到底是哪些原因形成的?通过事先安排好的计划,有规律地去收集生产过程中的有关数据,通过统计分析,我们不但要弄清楚变异是由哪几部分原因组成,而且要定量地给出每部分原因所产生的变异究竟在总变异中占多大的比例。我们要找出产生变异的“罪魁祸首”,并把所有对产生变异有“贡献”的因素,按其对产生总变异的“贡献率”排成队,定量地列出一个需要解决的问题的顺序清单,以便在选择攻关项目时作为参考依据,这种分析方法就是我们所说的变异源分析,这一块内容在蓝皮书上有详细介绍(参见蓝皮书第三版第9章)。变异源分析是一个很大的课题,我们今天通过一个简单的案例强调一下它的重要性。
案例
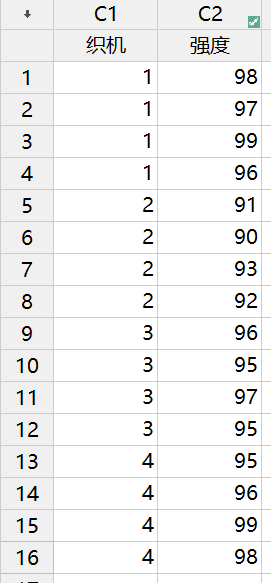
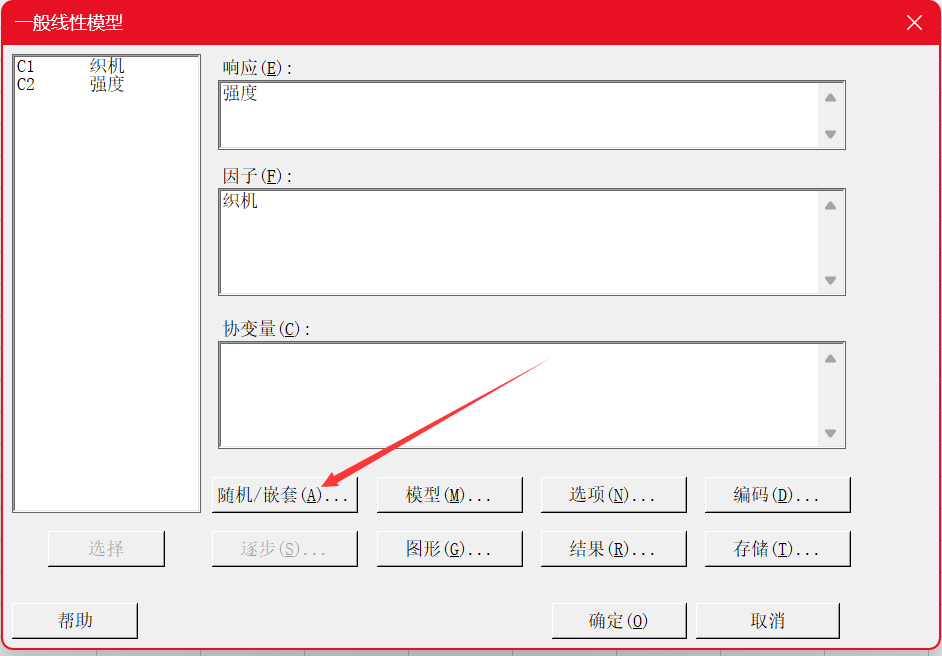
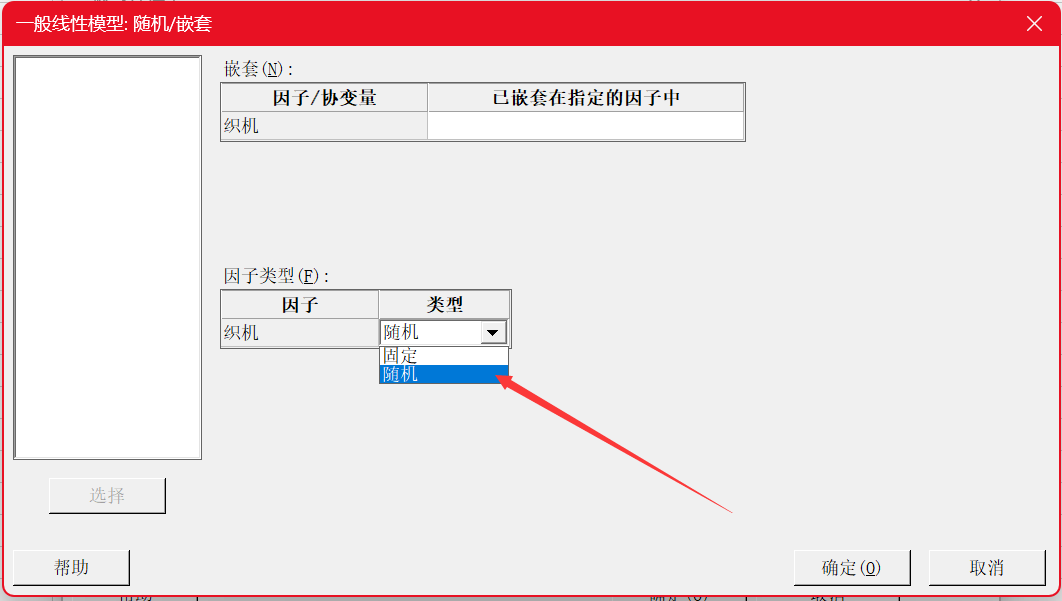
一家纺织厂用许多台织机编织一种织物,希望织机尽量相同使得织物的强度一致。过程工程师怀疑除了同一台织机编织的织物间强度会有差异外,在不同的织机间织物的强度也有显著差异。为此,她随机选择了4台织机并对每台织机生产的织物进行了4次强度测量,实验按随机顺序进行,数据如下所示:
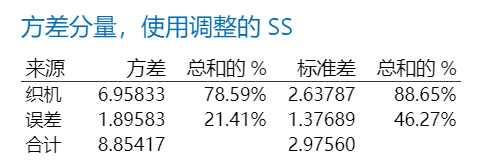
在输出结果中,我们主要关注的是方差分量这一块。我们可以看到任一强度观测的方差为8.85417(标准差2.97560),其中大部分的变异来源于织机间的差异(方差为6.95833,标准差为2.63786),占总变异比率为78.59%,剩下变异全归随机误差方差为1.89583(标准差为1.37689),占总变异比率为21.41%.
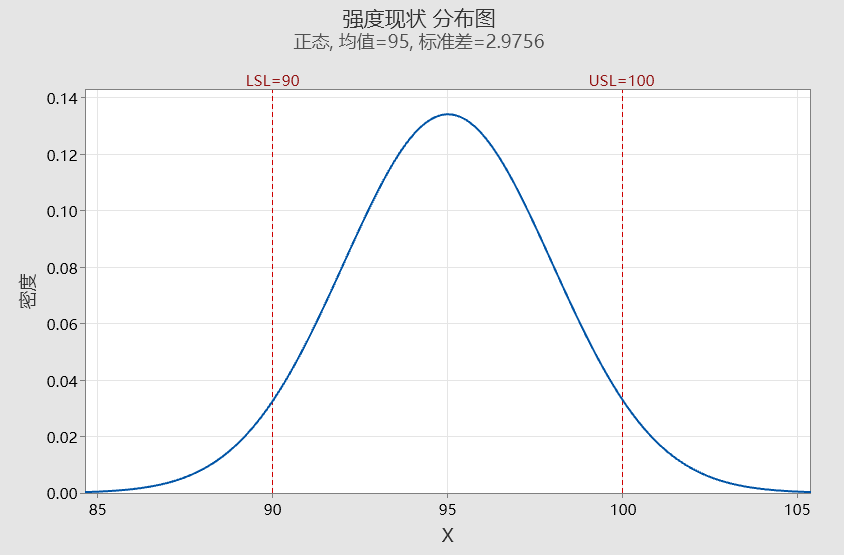
这个案例的操作和解释到此结束,现在我们再回到文章的开头。学变异源分析不是让大家热衷对方差分析的深入研究,比如这里方差分量的计算,而是要去对过程变异的关注。现在强度的变异非常大,过程不良率非常高,如下图所示:
容易看出,过程输出中有相当大的比例落在规格限之外。过程工程师疑虑为什么这么多的织物不合格,需要报废、返修或降格为低质量产品。答案是产品强度的差异主要源于织机间的差异,织机间性能的差异可能源于错误的设置、缺乏保养、缺少监管、操作员技术差、原材料有问题等。过程工程师现在需要去现场查找造成织机性能差异的具体原因,若她能找出并消除织机间差异的根源,过程产出的标准差就可以明显减少,也许可以低到1.37689,如下图所示。虽然不太可能根除织机间的所有差异,但是,方差分量的明显减小显然能大大提高所产织物的质量。
其实,看上图和方差分量的结果,我们可以看出来,即使通过改善把织机的变异源消除,剩下的变异还是很大(变异占比21.41%),说明还可能存在其他变异来源,所以把织机问题解决后我们还要进一步分析。
吐槽一下
变异源分析背后理论涉及到方差分量的计算,详细推导可以参考蒙哥马利的《实验设计与分析》,但我在这里也不得不说一下很多朋友就是因为看书才放弃了这一块内容的研究学习,原因很简单:公式太复杂,然而计算这一块我们交给Minitab软件就行了。我们需要做的是在前期:变异来源有哪些?这些因子是随机还是固定?这些因子之间的关系是交叉还是嵌套?基于这些问题再去制定数据收集计划,计算交给软件,我们会解读结果即可。
另外,变异源分析也是我们常用工具(如MSA、SPC和DOE等)的基础,没有变异源的调查这些分析可以说是毫无意义。 收起阅读 »
让标准差尽可能小不是件简单的事,它可能牵涉生产中的很多因素。生产中产生的变异这么大,到底是哪些原因形成的?通过事先安排好的计划,有规律地去收集生产过程中的有关数据,通过统计分析,我们不但要弄清楚变异是由哪几部分原因组成,而且要定量地给出每部分原因所产生的变异究竟在总变异中占多大的比例。我们要找出产生变异的“罪魁祸首”,并把所有对产生变异有“贡献”的因素,按其对产生总变异的“贡献率”排成队,定量地列出一个需要解决的问题的顺序清单,以便在选择攻关项目时作为参考依据,这种分析方法就是我们所说的变异源分析,这一块内容在蓝皮书上有详细介绍(参见蓝皮书第三版第9章)。变异源分析是一个很大的课题,我们今天通过一个简单的案例强调一下它的重要性。
案例
一家纺织厂用许多台织机编织一种织物,希望织机尽量相同使得织物的强度一致。过程工程师怀疑除了同一台织机编织的织物间强度会有差异外,在不同的织机间织物的强度也有显著差异。为此,她随机选择了4台织机并对每台织机生产的织物进行了4次强度测量,实验按随机顺序进行,数据如下所示:
在输出结果中,我们主要关注的是方差分量这一块。我们可以看到任一强度观测的方差为8.85417(标准差2.97560),其中大部分的变异来源于织机间的差异(方差为6.95833,标准差为2.63786),占总变异比率为78.59%,剩下变异全归随机误差方差为1.89583(标准差为1.37689),占总变异比率为21.41%.
这个案例的操作和解释到此结束,现在我们再回到文章的开头。学变异源分析不是让大家热衷对方差分析的深入研究,比如这里方差分量的计算,而是要去对过程变异的关注。现在强度的变异非常大,过程不良率非常高,如下图所示:
容易看出,过程输出中有相当大的比例落在规格限之外。过程工程师疑虑为什么这么多的织物不合格,需要报废、返修或降格为低质量产品。答案是产品强度的差异主要源于织机间的差异,织机间性能的差异可能源于错误的设置、缺乏保养、缺少监管、操作员技术差、原材料有问题等。过程工程师现在需要去现场查找造成织机性能差异的具体原因,若她能找出并消除织机间差异的根源,过程产出的标准差就可以明显减少,也许可以低到1.37689,如下图所示。虽然不太可能根除织机间的所有差异,但是,方差分量的明显减小显然能大大提高所产织物的质量。
其实,看上图和方差分量的结果,我们可以看出来,即使通过改善把织机的变异源消除,剩下的变异还是很大(变异占比21.41%),说明还可能存在其他变异来源,所以把织机问题解决后我们还要进一步分析。
吐槽一下
变异源分析背后理论涉及到方差分量的计算,详细推导可以参考蒙哥马利的《实验设计与分析》,但我在这里也不得不说一下很多朋友就是因为看书才放弃了这一块内容的研究学习,原因很简单:公式太复杂,然而计算这一块我们交给Minitab软件就行了。我们需要做的是在前期:变异来源有哪些?这些因子是随机还是固定?这些因子之间的关系是交叉还是嵌套?基于这些问题再去制定数据收集计划,计算交给软件,我们会解读结果即可。
另外,变异源分析也是我们常用工具(如MSA、SPC和DOE等)的基础,没有变异源的调查这些分析可以说是毫无意义。 收起阅读 »
半导体制造商提高质量和产量的 4 个步骤
半导体制造不仅是技术最先进的行业之一,而且也是成本最密集的行业之一。随着基于半导体的设备在从个人电脑到电话和汽车的一切事物中变得司空见惯,需求持续增长。随着数量的增加,对更强大的质量计划的需求也在增加。虽然大多数制造商都在使用 Minitab 等统计软件来解决某些问题,但仍有机会扩大其范围并提供更多价值。
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
Minitab 分析揭示了顶级度假租赁提供商令人惊讶的旅行者偏好
TELUS International 是一家为全球客户提供多语言数字客户体验和数字 IT 解决方案的提供商。客户包括技术和游戏、通信和媒体、电子商务和金融科技、旅游和酒店以及医疗保健领域的公司。
COVID-19 大流行给许多行业带来了沉重打击——旅游和酒店业是受灾最严重的行业之一。我们的一位客户在世界各地出租度假屋和梦想之地,立即受到旅游业停摆的影响。该公司将大部分客户服务外包给 TELUS International。
管理大量取消的预订
当隔离和规定突然变得不可能时,我们的客户不得不管理所有被取消的预订,这既不是业主的错,也不是旅客的错。这种情况的性质是前所未有的。对于取消,没有千篇一律的解决方案。由于预订时的政策和协议,部分旅客无法获得全额退款;任何给定情况都有不同程度的退款。
尽管取消预订既不是由我们的客户也不是客人造成的,但我们发现在此期间客户满意度评级出现了惊人的下降。我们特别感兴趣的是,客户对情况的管理方式而不是取消的结果不满意。
检验假设以改善客户体验
我们开始问,“我们怎样才能让它变得更好”?从技术的角度来看,我们的客户使用一流的 AI 技术来确保捕获、存储问题并向座席提出建议,以便在他们下次联系时解决客户的问题,无论是聊天、电子邮件还是电话. 然而,我们注意到最大的诋毁者来自聊天和电子邮件。
考虑到行业从客户满意度到客户努力的转变,这是令人惊讶的。在这个基于应用程序的人群中拜访客户被认为是浪费时间,他们宁愿在做其他更有意义的事情时聊天并解决他们的问题。我们认为我们一直在为客户提供他们想要的东西:一种“非接触式”客户支持方式。
是时候重新考虑我们一直在做的一切了。这就是 Minitab 成为我们宝贵工具的地方。使用 Minitab,我们能够执行假设检验以找到不满意的客户服务评论的根本原因。我们获得的分析和见解是出乎意料的,但我们坚信它是准确的并且反映了旅行者的需求。
最后,我们能够与领导团队分享我们的 Minitab 分析。因此,进行了新技术投资,为公司的代理商和整个客户服务团队提供了全新的方法和方向。
收起阅读 »
DMAIC、DMADV 与 DFSS:六西格玛术语指南
当您学习六西格玛时,熟悉各种首字母缩写词和缩略词可能会让您感到困难重重。从 FMEA 和 C&E 矩阵到量具 R&R 和 SIPOC… 术语清单没完没了!DMAIC、DMADV 和 DFSS 可能尤其难懂,因为它们听起来非常相似。但没关系。我们可以帮助您理解!DFSS、DMAIC 和 DMADV 可帮助质量改进从业者专注于项目重点,按既定路线完成项目。每个字母表示过程中的一个步骤。
从 DFSS 和 DMADV 开始首先,DFSS 表示“六西格玛设计”(DESIGN FOR SIX SIGMA),它专注于创建新产品或过程,或者通过六西格玛项目完全重新设计产品或过程。DMADV 是许多企业和组织常用的 DFSS 类型。
DMADV 表示:
定义 (Define): 定义过程和设计目标。
测量 (Measure):测量(并确定)过程/产品的关键质量特性方面,包括风险和生产能力。
分析 (Analyze):进行分析以制定设计过程,并进行评估以便为过程选择最佳设计。
设计 (Design) :设计过程详细信息,优化和检验设计。
验证 (Verify):使用试点检验来验证为过程选择的设计。实施和监控新过程。
聚焦 DMAIC:
DMAIC 是一种著名的六西格玛项目方法,其重点是改进现有的过程,而不是像 DFSS 或 DMADV 那样,专注于创建新产品或过程或者完全重新设计。一般来说,DMAIC 方法可以包括在其他过程改进计划(如精益)中,也可以自行制定。
DMAIC 表示:
定义 (Define) :定义产品或过程问题。
测量 (Measure):测量当前过程并收集数据。
分析 (Analyze):分析数据以找出缺陷的根本原因。
改进 (Improve):基于数据分析结果改进过程,并对过程进行检验。(本阶段中经常使用 DOE 等技术)。
控制 (Control):控制新过程并监控缺陷。(统计过程控制技术在本阶段非常有用)。
选择项目时着眼于 DMAIC
在出色的项目选择方法中,一个重要的组成部分是选择最有可能从 DMAIC 方法受益的项目,这意味着可以准确地测量项目所涉及的缺陷或过程中的变更。如果没有测量,将无法检测任何改进。一旦确定了项目重点,您就可以开始识别和定义要解决的问题。有关此过程的更多信息,请查看 DMAIC 工具和技术:“定义”阶段。无论您使用的是 DMAIC 还是 DMADV,这些方法的真正好处在于它们可以提供结构化问题解决方法来确保成功。当这些信息在 Minitab Engage 等解决方案中可用时,分享经验变得前所未有简单。可以快速、无缝地创建自定义路线图,以包括质量团队所需的任何其他步骤,并将这些步骤转化成未来项目的模板,从而节省时间并轻松地重复创建相同的路线图。 收起阅读 »
从 DFSS 和 DMADV 开始首先,DFSS 表示“六西格玛设计”(DESIGN FOR SIX SIGMA),它专注于创建新产品或过程,或者通过六西格玛项目完全重新设计产品或过程。DMADV 是许多企业和组织常用的 DFSS 类型。
DMADV 表示:
定义 (Define): 定义过程和设计目标。
测量 (Measure):测量(并确定)过程/产品的关键质量特性方面,包括风险和生产能力。
分析 (Analyze):进行分析以制定设计过程,并进行评估以便为过程选择最佳设计。
设计 (Design) :设计过程详细信息,优化和检验设计。
验证 (Verify):使用试点检验来验证为过程选择的设计。实施和监控新过程。
聚焦 DMAIC:
DMAIC 是一种著名的六西格玛项目方法,其重点是改进现有的过程,而不是像 DFSS 或 DMADV 那样,专注于创建新产品或过程或者完全重新设计。一般来说,DMAIC 方法可以包括在其他过程改进计划(如精益)中,也可以自行制定。
DMAIC 表示:
定义 (Define) :定义产品或过程问题。
测量 (Measure):测量当前过程并收集数据。
分析 (Analyze):分析数据以找出缺陷的根本原因。
改进 (Improve):基于数据分析结果改进过程,并对过程进行检验。(本阶段中经常使用 DOE 等技术)。
控制 (Control):控制新过程并监控缺陷。(统计过程控制技术在本阶段非常有用)。
选择项目时着眼于 DMAIC
在出色的项目选择方法中,一个重要的组成部分是选择最有可能从 DMAIC 方法受益的项目,这意味着可以准确地测量项目所涉及的缺陷或过程中的变更。如果没有测量,将无法检测任何改进。一旦确定了项目重点,您就可以开始识别和定义要解决的问题。有关此过程的更多信息,请查看 DMAIC 工具和技术:“定义”阶段。无论您使用的是 DMAIC 还是 DMADV,这些方法的真正好处在于它们可以提供结构化问题解决方法来确保成功。当这些信息在 Minitab Engage 等解决方案中可用时,分享经验变得前所未有简单。可以快速、无缝地创建自定义路线图,以包括质量团队所需的任何其他步骤,并将这些步骤转化成未来项目的模板,从而节省时间并轻松地重复创建相同的路线图。 收起阅读 »
5个更重要的精益工具
尽管精益源于制造业,但世界上几乎每个行业和所有类型的组织都可以从中受益。不久前,我们回顾了5个关键精益工具这是开始实施精益的好方法。今天,让我们继续学习5种更重要的精益工具。
1.改善
改善是一种加速流程改进项目的方法。虽然最初是为制造业开发的,但改善广泛应用于各种行业,对于流程改进实践者来说是一项有价值的技术。改善是一项为期3-5天的专项活动,旨在推动流程改进。员工被从日常工作中抽出来参与。立即实施解决方案。领导者使用上述参与路线图来更好地计划和实施改善活动。
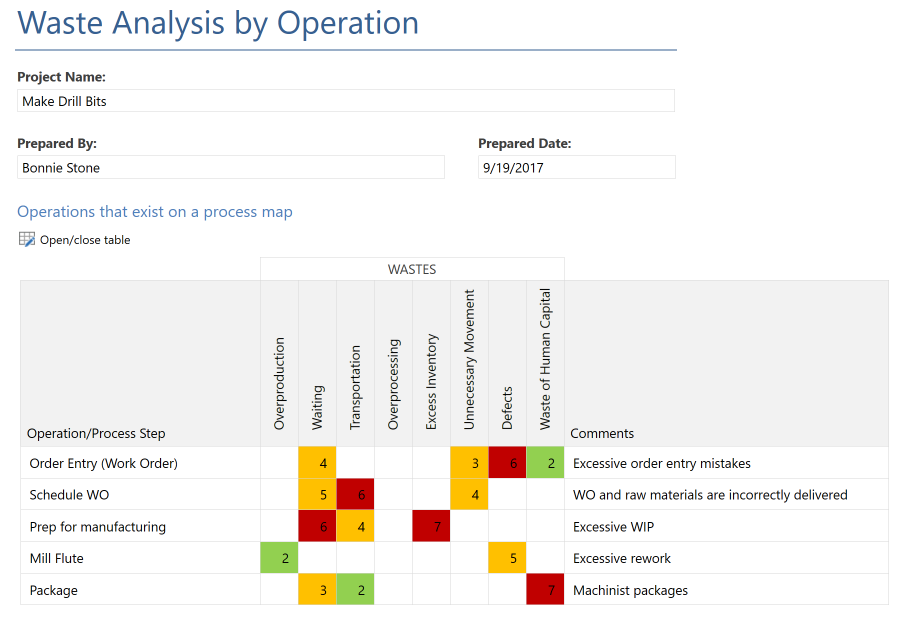
2.废物分析
在精益生产中,浪费是指流程中任何不必要的、从客户角度看不会增加价值的东西。精益的目的是识别、分析和消除所有的浪费来源,如缺陷或过量库存。
使用Minitab Engage的“按操作进行废物分析”表格来记录每个过程步骤中的废物类型,并对废物的程度进行量化和颜色编码。当由多个观察者执行时,废物分析活动是最有效的,无论是在被检查的过程之内还是之外。
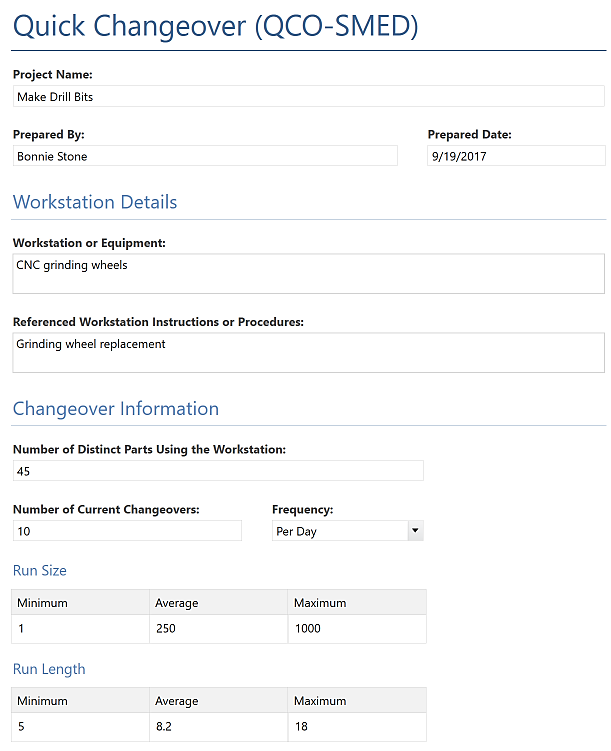
3.快速转换
快速转换是一种分析过程的方法,可以减少设置所需的时间、技术资源或材料。最初这种技术应用于制造环境,特别是工具和模具。最近,这种方法已经应用于各种需要快速重置的工作流(包括交易流程),如医院病床、手术室或装卸飞机乘客。快速转换包括识别过程步骤,并将每个步骤分配到两个类别中的一个:
内部-必须在进程停止时完成,并且
外部-可以在流程运行时完成,在执行设置之前或之后。
使用快速转换(QCO-SMED)表单来比较当前和改进状态的流程转换或设置的内部和外部组件。通过实施快速转换,组织可以减少内部设置时间,从而减少非生产性流程时间,并实现更多设置、更小的运行批次和改进的流程。第二个目标是减少总的准备时间,以释放劳动力。
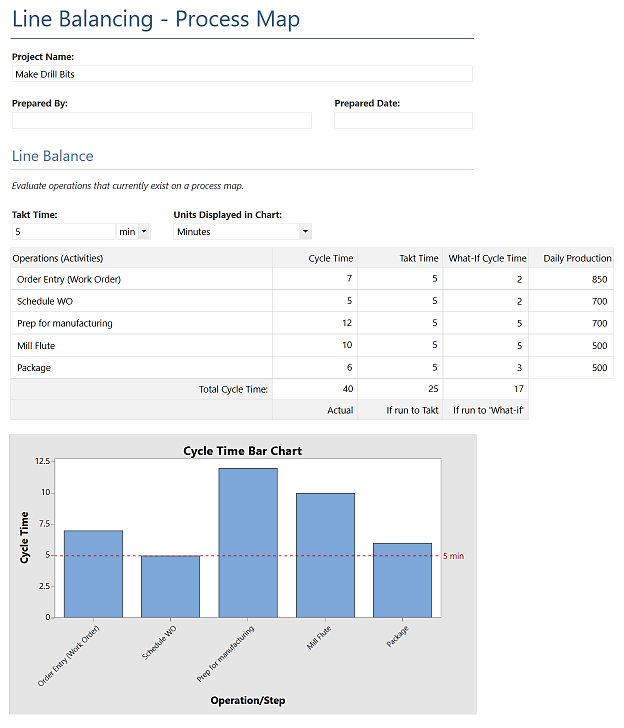
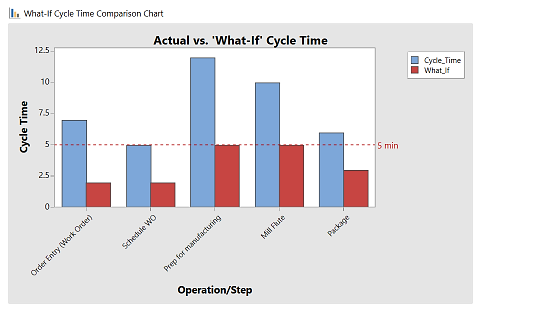
4.人工投入线性平衡法
生产线平衡是一种“均衡”一组过程步骤的技术,以平滑完成这些步骤所需的时间。当流程步骤不平衡时,可能会出现一个或多个约束或瓶颈。
目标是消除非增值任务,合并任务并密切平衡剩余步骤,以便所有步骤都满足客户需求率。使用Minitab Engage的生产线平衡-流程图或生产线平衡-价值流图表格,将流程图或价值流图上多个操作的周期时间与生产节拍时间(满足客户需求所需的时间)进行比较。
当您试图平衡一个单元或一系列连续的过程步骤时,这种分析是有用的。它凸显了等待的浪费。
5.标准工作
标准化工作建立了一套工作程序,为流程提供了最佳、最可靠的方法和顺序。标准化工作阐明了流程,记录了完成工作的最佳方式,确保了一致性,加快了员工培训,并为进一步改进提供了基准。
使用Minitab Engage的标准工作组合图表表格显示与每个工作要素相关的手动、机器和行走时间。输出以图形方式将累计时间显示为手动(操作员控制)时间、机器时间和行走时间。查看综合数据有助于识别过度运动和等待造成的浪费。
你可以去看看Minitab Engage在线帮助要观看视频,请了解有关这些工具的更多信息,并下载30天免费试用版亲自试用。在此评论或让我们知道脸谱网或者推特如果您有任何问题或其他您希望我们涵盖的领域。
收起阅读 »
1.改善
改善是一种加速流程改进项目的方法。虽然最初是为制造业开发的,但改善广泛应用于各种行业,对于流程改进实践者来说是一项有价值的技术。改善是一项为期3-5天的专项活动,旨在推动流程改进。员工被从日常工作中抽出来参与。立即实施解决方案。领导者使用上述参与路线图来更好地计划和实施改善活动。
2.废物分析
在精益生产中,浪费是指流程中任何不必要的、从客户角度看不会增加价值的东西。精益的目的是识别、分析和消除所有的浪费来源,如缺陷或过量库存。
使用Minitab Engage的“按操作进行废物分析”表格来记录每个过程步骤中的废物类型,并对废物的程度进行量化和颜色编码。当由多个观察者执行时,废物分析活动是最有效的,无论是在被检查的过程之内还是之外。
3.快速转换
快速转换是一种分析过程的方法,可以减少设置所需的时间、技术资源或材料。最初这种技术应用于制造环境,特别是工具和模具。最近,这种方法已经应用于各种需要快速重置的工作流(包括交易流程),如医院病床、手术室或装卸飞机乘客。快速转换包括识别过程步骤,并将每个步骤分配到两个类别中的一个:
内部-必须在进程停止时完成,并且
外部-可以在流程运行时完成,在执行设置之前或之后。
使用快速转换(QCO-SMED)表单来比较当前和改进状态的流程转换或设置的内部和外部组件。通过实施快速转换,组织可以减少内部设置时间,从而减少非生产性流程时间,并实现更多设置、更小的运行批次和改进的流程。第二个目标是减少总的准备时间,以释放劳动力。
4.人工投入线性平衡法
生产线平衡是一种“均衡”一组过程步骤的技术,以平滑完成这些步骤所需的时间。当流程步骤不平衡时,可能会出现一个或多个约束或瓶颈。
目标是消除非增值任务,合并任务并密切平衡剩余步骤,以便所有步骤都满足客户需求率。使用Minitab Engage的生产线平衡-流程图或生产线平衡-价值流图表格,将流程图或价值流图上多个操作的周期时间与生产节拍时间(满足客户需求所需的时间)进行比较。
当您试图平衡一个单元或一系列连续的过程步骤时,这种分析是有用的。它凸显了等待的浪费。
5.标准工作
标准化工作建立了一套工作程序,为流程提供了最佳、最可靠的方法和顺序。标准化工作阐明了流程,记录了完成工作的最佳方式,确保了一致性,加快了员工培训,并为进一步改进提供了基准。
使用Minitab Engage的标准工作组合图表表格显示与每个工作要素相关的手动、机器和行走时间。输出以图形方式将累计时间显示为手动(操作员控制)时间、机器时间和行走时间。查看综合数据有助于识别过度运动和等待造成的浪费。
你可以去看看Minitab Engage在线帮助要观看视频,请了解有关这些工具的更多信息,并下载30天免费试用版亲自试用。在此评论或让我们知道脸谱网或者推特如果您有任何问题或其他您希望我们涵盖的领域。
收起阅读 »
密封处理:波士顿科学Heredia验证包装过程的变化
当世界各地的医生依靠你的产品来诊断和治疗无数的病人时,你需要确保这些产品是安全的,并且尽可能负担得起。
这就是为什么波士顿科学Heredia定期评估其运营,以保持流程效率,并通过降低成本为负担得起的医疗保健做出贡献。30多年来,波士顿科技公司一直致力于医疗技术的开发、制造和营销,并为各种医疗专业提供服务。
在其哥斯达黎加的Heredia工厂,包装工程师Daniel Calvo Camacho领导了一项简化导丝包装的工作,推出了一种新的更小的塑料袋,导丝用于导管放置或内窥镜诊断等程序。
该工厂的工程师使用Minitab统计软件来帮助评估和验证他们的包装过程,这使得Boston Scientific能够满怀信心地继续对其包装袋进行成本节约的重新设计。
挑战
为他们的Amplatz超硬导丝使用更小和不同的包装材料将大大降低波士顿科技公司的材料成本,但该公司需要确保新的小袋能够与他们的密封过程配合使用,这就形成了一个屏障,使导丝在准备使用前保持无菌。
波士顿科学公司哥斯达黎加工厂的一个项目团队使用Minitab统计软件来分析数据,以验证用于医疗程序的导丝包装的封袋过程。上图中,导丝装在一个袋子里,准备密封。
在洁净室中,操作人员将导丝装入袋中,然后将袋倒置在密封传送带上。每个袋子的开放边缘通过前后带之间的热量和压力,创造一个可剥离的密封。
包装工程师需要确保小包装袋的密封强度仍然达到或超过标准。他们评估了该过程,并确定了几个输入变量,其中包括密封系统的前后加热带的温度和系统的速度。
现在,该小组需要评估这些变量中的每一个,并确定它们如何影响小袋密封的质量。哪些输入是最重要的?操作人员应该在哪里设置系统的温度和速度,以确保每个袋子都有牢固的密封?
Minitab如何帮助
这就是被称为实验设计的统计方法的用武之地。一个设计好的实验让你一次同时改变和评估一个以上的输入变量,然后使用统计分析得到关于所有感兴趣的输入变量的有意义的结果。您可以快速确定哪些因素很重要,然后调整过程以获得所需的结果。
Minitab统计软件可用于轻松创建和分析多种设计实验。Calvo Camacho使用它创建了一个两级全因子设计的实验,这将使团队能够评估所有的输入变量以及它们之间的双向交互作用。
“在评估了创建DOE的初步过程参数后,我选择了不同的因素和这些因素的水平,这将有助于团队执行我们的实验,”Calvo Camacho说。然后,团队开始收集实验数据。Minitab的DOE工具创建了一个运行列表,每个运行指定了每个因子的两个水平的不同组合。操作员为每个实验条件制作了一个样本海豹,然后卡尔沃·卡马乔和他的团队测量了每个海豹的强度。在完成所有实验运行后,他使用Minitab分析结果。
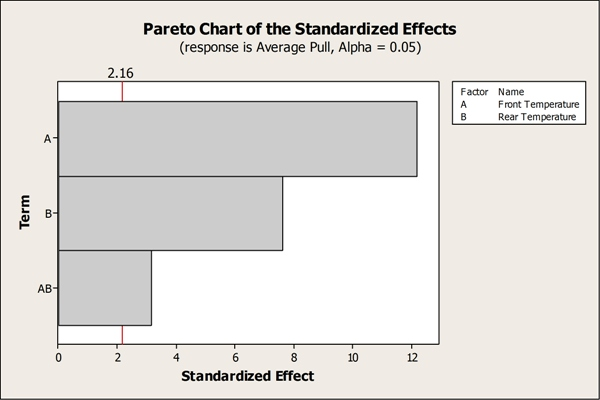
该分析将前方和后方的温度确定为重要因素,以及它们之间的双向相互作用。速度不是影响密封强度的重要因素,这使得研究小组可以将其从模型中移除。传统的一次一个因素(OFAT)实验可能很容易错过导致长期过程控制问题的重要相互作用。
上面的帕累托图确定了显著影响密封强度的因素:前部温度、后部温度以及它们各自的双向相互作用。
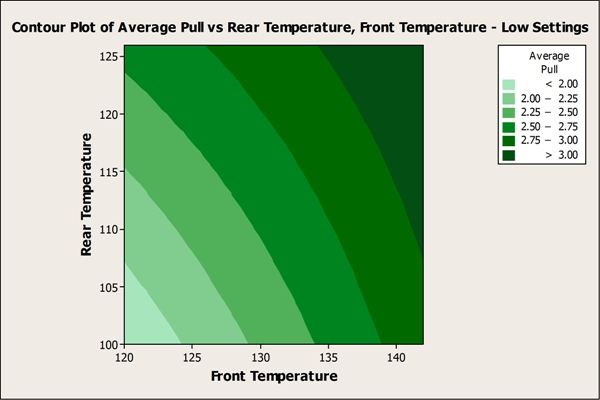
该团队还使用Minitab创建等高线图,揭示密封强度达到或超过规格的温度范围。
通过关注设计实验中确定的关键因素,该团队设计了最佳的工艺设置,以确保新的包装袋具有牢固的密封。现在,他们转向Minitab,用一种叫做能力分析的工具来验证新工艺设置的有效性,这种工具可以证明工艺是否符合规范,是否能够生产出好的零件。他们使用他们确定的最佳过程设置来密封包装袋,记住温度越高,密封越强。然后,他们测量这些包装袋的密封强度,并进行能力分析,以评估相对于规格下限的测量值。他们的能力分析表明,建议的温度设置符合甚至超过了最低密封强度要求。
该团队在Minitab中执行过程能力分析,这有助于他们证明提议的温度设置将允许他们实现最终生产目标。
通过实验和使用Minitab统计软件进行的数据分析,该团队能够证明他们的包装系统以高效的方式运行,并将继续使用新的包装袋。
结果
现在,仔细的数据分析显示了密封系统的有效性,哥斯达黎加的工厂可以开始使用新的塑料袋,这将导致大量的节约。“我们每年都会评估我们的流程,以不断提高质量和服务,但我们也积极寻求降低成本的机会,”Calvo Camacho说。
采用新的邮袋支持波士顿科学的更广泛的努力,以简化整个公司的包装,该项目发挥了重要作用,该公司的综合节省超过330,000美元至今。此外,该团队的流程验证确认了这些变化和节约是可以持续的。这对公司来说是个好消息,最终对依赖他们产品的医生和病人来说也是。
“最终,”卡尔沃·卡马乔指出,“我们存的钱越多,我们就能把更多的储蓄传递给我们服务的人。” 收起阅读 »
这就是为什么波士顿科学Heredia定期评估其运营,以保持流程效率,并通过降低成本为负担得起的医疗保健做出贡献。30多年来,波士顿科技公司一直致力于医疗技术的开发、制造和营销,并为各种医疗专业提供服务。
在其哥斯达黎加的Heredia工厂,包装工程师Daniel Calvo Camacho领导了一项简化导丝包装的工作,推出了一种新的更小的塑料袋,导丝用于导管放置或内窥镜诊断等程序。
该工厂的工程师使用Minitab统计软件来帮助评估和验证他们的包装过程,这使得Boston Scientific能够满怀信心地继续对其包装袋进行成本节约的重新设计。
挑战
为他们的Amplatz超硬导丝使用更小和不同的包装材料将大大降低波士顿科技公司的材料成本,但该公司需要确保新的小袋能够与他们的密封过程配合使用,这就形成了一个屏障,使导丝在准备使用前保持无菌。
波士顿科学公司哥斯达黎加工厂的一个项目团队使用Minitab统计软件来分析数据,以验证用于医疗程序的导丝包装的封袋过程。上图中,导丝装在一个袋子里,准备密封。
在洁净室中,操作人员将导丝装入袋中,然后将袋倒置在密封传送带上。每个袋子的开放边缘通过前后带之间的热量和压力,创造一个可剥离的密封。
包装工程师需要确保小包装袋的密封强度仍然达到或超过标准。他们评估了该过程,并确定了几个输入变量,其中包括密封系统的前后加热带的温度和系统的速度。
现在,该小组需要评估这些变量中的每一个,并确定它们如何影响小袋密封的质量。哪些输入是最重要的?操作人员应该在哪里设置系统的温度和速度,以确保每个袋子都有牢固的密封?
Minitab如何帮助
这就是被称为实验设计的统计方法的用武之地。一个设计好的实验让你一次同时改变和评估一个以上的输入变量,然后使用统计分析得到关于所有感兴趣的输入变量的有意义的结果。您可以快速确定哪些因素很重要,然后调整过程以获得所需的结果。
Minitab统计软件可用于轻松创建和分析多种设计实验。Calvo Camacho使用它创建了一个两级全因子设计的实验,这将使团队能够评估所有的输入变量以及它们之间的双向交互作用。
“在评估了创建DOE的初步过程参数后,我选择了不同的因素和这些因素的水平,这将有助于团队执行我们的实验,”Calvo Camacho说。然后,团队开始收集实验数据。Minitab的DOE工具创建了一个运行列表,每个运行指定了每个因子的两个水平的不同组合。操作员为每个实验条件制作了一个样本海豹,然后卡尔沃·卡马乔和他的团队测量了每个海豹的强度。在完成所有实验运行后,他使用Minitab分析结果。
该分析将前方和后方的温度确定为重要因素,以及它们之间的双向相互作用。速度不是影响密封强度的重要因素,这使得研究小组可以将其从模型中移除。传统的一次一个因素(OFAT)实验可能很容易错过导致长期过程控制问题的重要相互作用。
上面的帕累托图确定了显著影响密封强度的因素:前部温度、后部温度以及它们各自的双向相互作用。
该团队还使用Minitab创建等高线图,揭示密封强度达到或超过规格的温度范围。
通过关注设计实验中确定的关键因素,该团队设计了最佳的工艺设置,以确保新的包装袋具有牢固的密封。现在,他们转向Minitab,用一种叫做能力分析的工具来验证新工艺设置的有效性,这种工具可以证明工艺是否符合规范,是否能够生产出好的零件。他们使用他们确定的最佳过程设置来密封包装袋,记住温度越高,密封越强。然后,他们测量这些包装袋的密封强度,并进行能力分析,以评估相对于规格下限的测量值。他们的能力分析表明,建议的温度设置符合甚至超过了最低密封强度要求。
该团队在Minitab中执行过程能力分析,这有助于他们证明提议的温度设置将允许他们实现最终生产目标。
通过实验和使用Minitab统计软件进行的数据分析,该团队能够证明他们的包装系统以高效的方式运行,并将继续使用新的包装袋。
结果
现在,仔细的数据分析显示了密封系统的有效性,哥斯达黎加的工厂可以开始使用新的塑料袋,这将导致大量的节约。“我们每年都会评估我们的流程,以不断提高质量和服务,但我们也积极寻求降低成本的机会,”Calvo Camacho说。
采用新的邮袋支持波士顿科学的更广泛的努力,以简化整个公司的包装,该项目发挥了重要作用,该公司的综合节省超过330,000美元至今。此外,该团队的流程验证确认了这些变化和节约是可以持续的。这对公司来说是个好消息,最终对依赖他们产品的医生和病人来说也是。
“最终,”卡尔沃·卡马乔指出,“我们存的钱越多,我们就能把更多的储蓄传递给我们服务的人。” 收起阅读 »
如何使用模拟数据修复过程并改进产品开发?
当资源有限,或者收集真实数据过于昂贵或不切实际时,如何遵循现实的预测和时间表?模拟数据是否值得信任,可进行准确预测?这就是 Monte Carlo 模拟的用武之地。
然而,实际上,模拟数据通常用于许多场景,如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。Monte Carlo 模拟是一种数学建模技术,可允许您查看所有可能的结果并评估风险以做出数据驱动型决策。通过大量随机计算模拟运行历史数据,以预测未来项目在类似情况下的可能结果。
Minitab Engage 是一个软件平台,它将用于执行质量项目的桌面应用程序与 Web 控制台相结合,从而使报告整个质量计划变得易如反掌。Monte Carlo 模拟工具是桌面应用程序中的一流工具之一,它使模拟方法变得非常易于访问。
Monte Carlo 方法使用重复随机抽样来生成要用于数学模型的模拟数据。此模型通常来自统计分析(如实验设计或回归分析)。
假设您研究一个过程并使用统计量对其建模,如下所示:
使用这种类型的线性模型,可以将过程输入值输入到方程中并预测过程输出。但是,在现实世界中,由于变异性,输入值不会是单个值。不幸的是,这种输入变异性会导致输出中出现变异性和缺陷。
在考虑不确定性的同时设计更好的过程
为了设计更好的过程,您可以收集大量数据来确定在各种条件下输入变异性与输出变异性之间的关系。但是,如果您了解输入值的典型分布,并且您有一个对过程进行建模的方程,则可以轻松生成海量模拟输入值并将它们输入到过程方程中,以生成过程输出的模拟分布。
您还可以轻松更改这些输入分布以回答“如果…怎么办”类型的问题。这就是 Monte Carlo 模拟的全部内容。在即将介绍的 Minitab Engage 用法示例中,我们将更改模拟数据的均值和标准差以改进产品质量。
使用 Minitab Engage 进行 Monte Carlo 模拟的分步示例
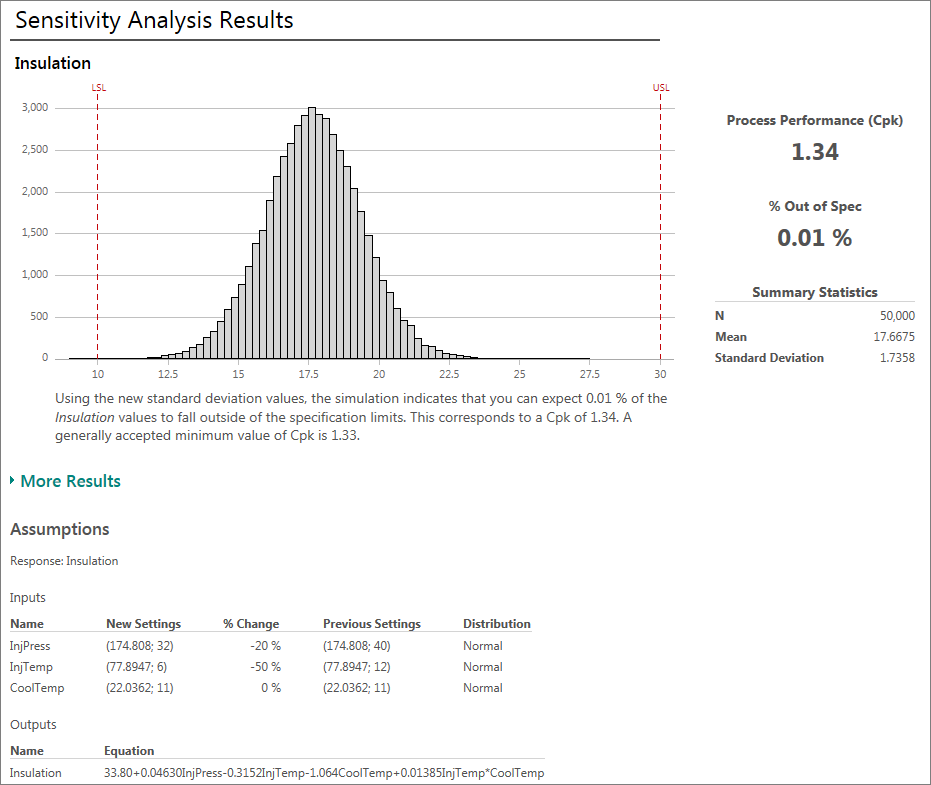
一家建筑产品制造商的材料工程师正在开发一种新的绝缘产品。
该工程师进行了一项试验并使用统计量来分析可能会影响产品绝缘效果的过程因子。对于这个 Monte Carlo 模拟示例,我们将使用上面显示的回归方程,该方程描述了过程中涉及的统计意义显著的因素。
步骤 1:定义过程输入和输出
我们需要做的第一件事是定义输入及其值的分布。
过程输入在回归输出中列出,工程师熟悉每个变量的典型均值和标准差。对于输出,工程师可以从 Minitab Statistical Software 复制用来描述过程的回归方程并将其粘贴到 Engage 的 Monte Carlo 工具中。
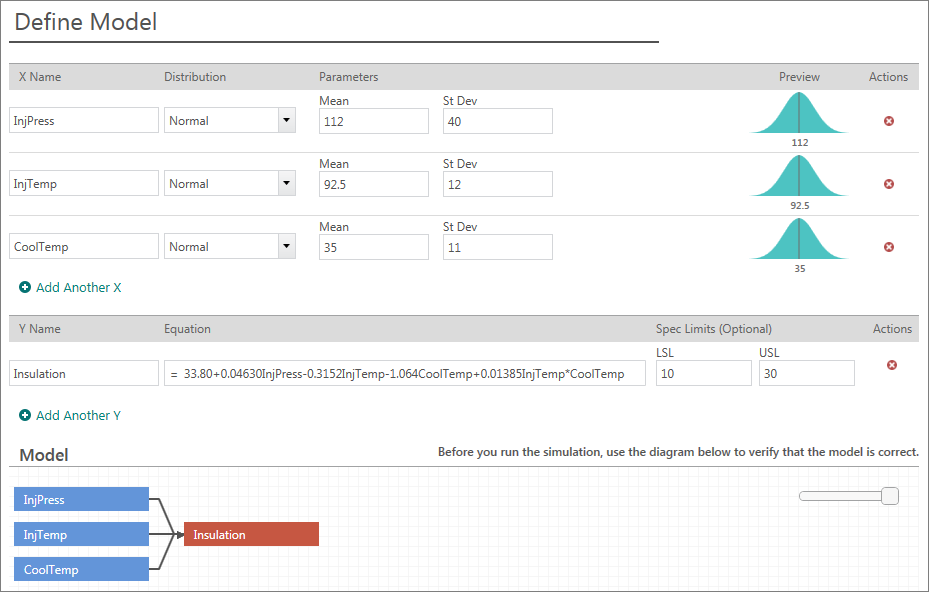
如下图所示,可以轻松键入过程相关输入和输出的信息。
验证模型,然后可以运行模拟(默认情况下,Engage 会以极快的速度运行 50,000 次模拟,但您可以指定更大或更小的次数值)。
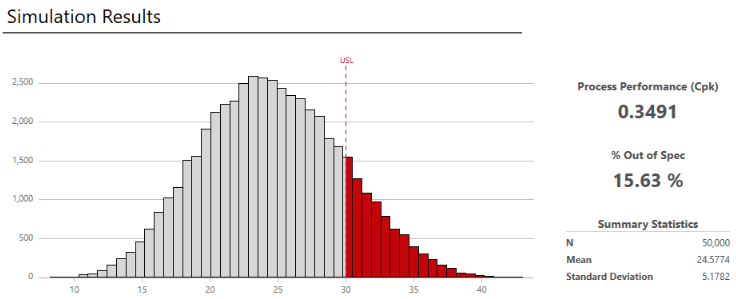
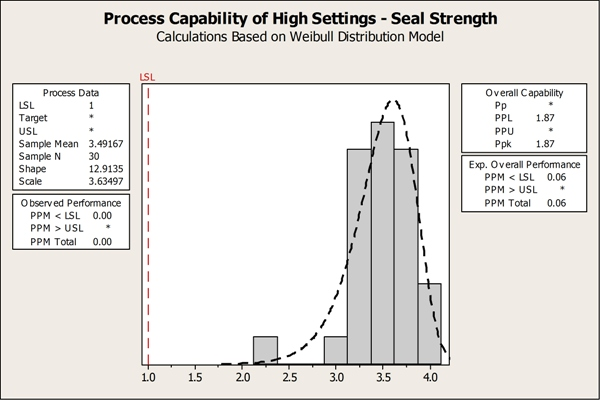
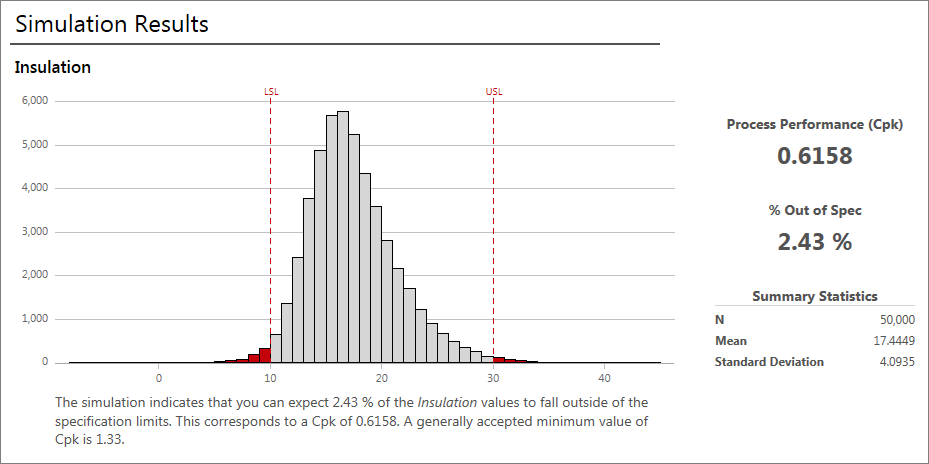
Engage 使用能力分析的典型输出(能力直方图、缺陷百分比和 Ppk 统计量)为您解释结果。它正确地指出我们的 Ppk 低于普遍接受的最小值。
Engage 不但运行模拟并让您确定后续做法,而且还确定过程不令人满意并提出一系列智能步骤来改进过程能力。
它还知道控制均值通常比控制变异性更容易。因此,Engage 提出的下一步是进行用来查找均值设置的参数优化,均值设置可在考虑输入变异性的同时最大限度地减少缺陷数量。
步骤 2:定义参数优化的目标和搜索范围
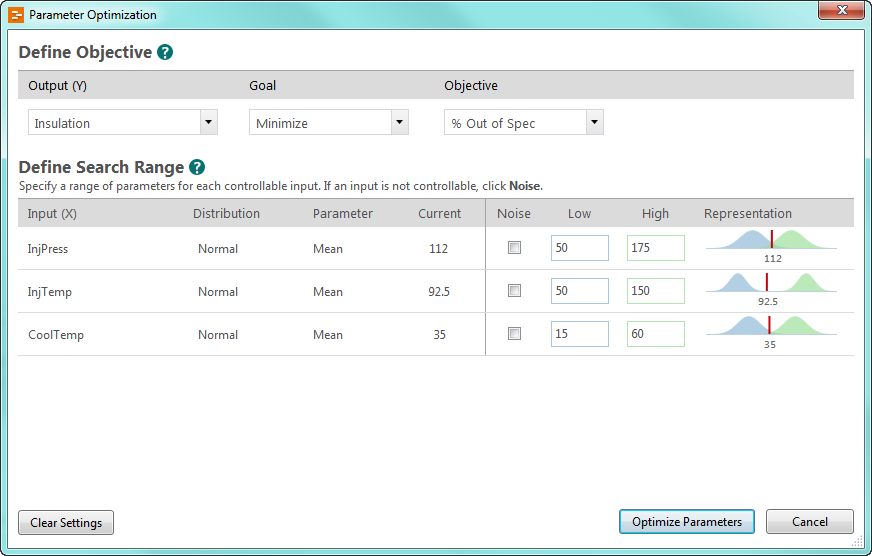
在这个阶段,我们希望 Engage 找到均值输入设置的最佳组合,以最大限度地减少缺陷。可以使用参数优化来指定目标并利用您的过程知识来定义输入变量的合理搜索范围。
下面是模拟结果。
一眼就可以看出缺陷百分比下降了。我们还可以在表中看到最佳输入设置。然而,我们的 Ppk 统计量仍低于普遍接受的最小值。幸运的是,Engage 为我们推荐了可进一步改进过程能力的后续步骤。
步骤 3:控制变异性以执行敏感度分析
到目前为止,我们已经通过优化均值输入设置来改进过程。这大大减少了缺陷,但我们在 Monte Carlo 模拟中还有更多工作要做。现在,我们需要减少过程输入的变异性以进一步减少缺陷。
减少变异性通常更难。因此,您不希望浪费资源来控制不会减少缺陷数量的输入的标准差。幸运的是,Engage 包含一个创新型图表,可帮助您确定在哪些输入中通过控制变异性可最大程度地减少缺陷数量。
在上图中,寻找带倾斜直线的输入,因为减小这些标准差可以降低输出中的变异性。相反,您可以放宽带平直直线的输入的公差,因为它们不会影响输出中的变异性。
在上图中,斜率基本相等。因此,我们将尝试减小几个输入的标准差。您需要利用过程知识来确定实际的减少量。要更改设置,可以单击线上的点,或使用表中的下拉菜单。
最终的 Monte Carlo 模拟结果
成功!过程中的缺陷数量有所减少,Ppk 统计量为 1.34 且高于基准值。该假定表向我们展示了应当尝试使用的过程输入的新设置和标准差。如果我们再次运行参数优化,它将成为过程的中心,我相信我们的缺陷会更少。
另外,所有这些都是在未收集任何进一步数据的情况下完成的,因为我们知道输入值的典型分布,并且有一个对过程进行建模的方程。 收起阅读 »
然而,实际上,模拟数据通常用于许多场景,如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。Monte Carlo 模拟是一种数学建模技术,可允许您查看所有可能的结果并评估风险以做出数据驱动型决策。通过大量随机计算模拟运行历史数据,以预测未来项目在类似情况下的可能结果。
Minitab Engage 是一个软件平台,它将用于执行质量项目的桌面应用程序与 Web 控制台相结合,从而使报告整个质量计划变得易如反掌。Monte Carlo 模拟工具是桌面应用程序中的一流工具之一,它使模拟方法变得非常易于访问。
Monte Carlo 方法使用重复随机抽样来生成要用于数学模型的模拟数据。此模型通常来自统计分析(如实验设计或回归分析)。
假设您研究一个过程并使用统计量对其建模,如下所示:
使用这种类型的线性模型,可以将过程输入值输入到方程中并预测过程输出。但是,在现实世界中,由于变异性,输入值不会是单个值。不幸的是,这种输入变异性会导致输出中出现变异性和缺陷。
在考虑不确定性的同时设计更好的过程
为了设计更好的过程,您可以收集大量数据来确定在各种条件下输入变异性与输出变异性之间的关系。但是,如果您了解输入值的典型分布,并且您有一个对过程进行建模的方程,则可以轻松生成海量模拟输入值并将它们输入到过程方程中,以生成过程输出的模拟分布。
您还可以轻松更改这些输入分布以回答“如果…怎么办”类型的问题。这就是 Monte Carlo 模拟的全部内容。在即将介绍的 Minitab Engage 用法示例中,我们将更改模拟数据的均值和标准差以改进产品质量。
使用 Minitab Engage 进行 Monte Carlo 模拟的分步示例
一家建筑产品制造商的材料工程师正在开发一种新的绝缘产品。
该工程师进行了一项试验并使用统计量来分析可能会影响产品绝缘效果的过程因子。对于这个 Monte Carlo 模拟示例,我们将使用上面显示的回归方程,该方程描述了过程中涉及的统计意义显著的因素。
步骤 1:定义过程输入和输出
我们需要做的第一件事是定义输入及其值的分布。
过程输入在回归输出中列出,工程师熟悉每个变量的典型均值和标准差。对于输出,工程师可以从 Minitab Statistical Software 复制用来描述过程的回归方程并将其粘贴到 Engage 的 Monte Carlo 工具中。
如下图所示,可以轻松键入过程相关输入和输出的信息。
验证模型,然后可以运行模拟(默认情况下,Engage 会以极快的速度运行 50,000 次模拟,但您可以指定更大或更小的次数值)。
Engage 使用能力分析的典型输出(能力直方图、缺陷百分比和 Ppk 统计量)为您解释结果。它正确地指出我们的 Ppk 低于普遍接受的最小值。
Engage 不但运行模拟并让您确定后续做法,而且还确定过程不令人满意并提出一系列智能步骤来改进过程能力。
它还知道控制均值通常比控制变异性更容易。因此,Engage 提出的下一步是进行用来查找均值设置的参数优化,均值设置可在考虑输入变异性的同时最大限度地减少缺陷数量。
步骤 2:定义参数优化的目标和搜索范围
在这个阶段,我们希望 Engage 找到均值输入设置的最佳组合,以最大限度地减少缺陷。可以使用参数优化来指定目标并利用您的过程知识来定义输入变量的合理搜索范围。
下面是模拟结果。
一眼就可以看出缺陷百分比下降了。我们还可以在表中看到最佳输入设置。然而,我们的 Ppk 统计量仍低于普遍接受的最小值。幸运的是,Engage 为我们推荐了可进一步改进过程能力的后续步骤。
步骤 3:控制变异性以执行敏感度分析
到目前为止,我们已经通过优化均值输入设置来改进过程。这大大减少了缺陷,但我们在 Monte Carlo 模拟中还有更多工作要做。现在,我们需要减少过程输入的变异性以进一步减少缺陷。
减少变异性通常更难。因此,您不希望浪费资源来控制不会减少缺陷数量的输入的标准差。幸运的是,Engage 包含一个创新型图表,可帮助您确定在哪些输入中通过控制变异性可最大程度地减少缺陷数量。
在上图中,寻找带倾斜直线的输入,因为减小这些标准差可以降低输出中的变异性。相反,您可以放宽带平直直线的输入的公差,因为它们不会影响输出中的变异性。
在上图中,斜率基本相等。因此,我们将尝试减小几个输入的标准差。您需要利用过程知识来确定实际的减少量。要更改设置,可以单击线上的点,或使用表中的下拉菜单。
最终的 Monte Carlo 模拟结果
成功!过程中的缺陷数量有所减少,Ppk 统计量为 1.34 且高于基准值。该假定表向我们展示了应当尝试使用的过程输入的新设置和标准差。如果我们再次运行参数优化,它将成为过程的中心,我相信我们的缺陷会更少。
另外,所有这些都是在未收集任何进一步数据的情况下完成的,因为我们知道输入值的典型分布,并且有一个对过程进行建模的方程。 收起阅读 »
使用变异图分析金融服务呼叫中心等待时间的原因
试图解决一个复杂的问题?您应该首先列出所有可疑变量。然后,确定少数关键因素,并将它们与其他对理解原因无关紧要的因素分开。让我们来看看一个非常简单的图形工具,它非常直观,几乎任何人都可以使用,并且不需要任何先验统计知识:变异性图表。
什么是变异图?
变异性图表是一种以可视化方式呈现方差分析 ( ANOVA ) 数据的好方法,它们在根本原因分析的早期阶段表现出色。它们的主要优势在于使您能够在单个图表中可视化许多不同的变化来源,同时提供因子效应的整体视图。
变异性图表可以帮助您在一张图表上进行调查和研究许多可能原因导致的变异模式。它们允许您显示过程中的位置或周期性变化。它们还可用于研究子组内、子组之间等的变异。
要在Minitab Statistical Software中创建变异性图表,请选择统计 > 质量工具 > 变异性图表... 然后在对话框中选择响应变量和最多八个因子。
使用变异图可视化呼叫中心等待时间
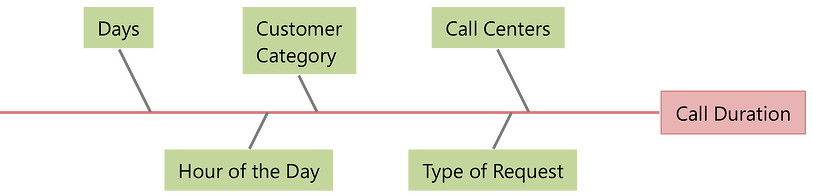
假设您需要检查来自一家大型金融服务公司的多个呼叫中心的等待时间。客户和潜在客户致电开立新账户、获取有关信用卡的信息、寻求技术支持和访问其他服务。您有关于客户类别、服务类型(请求)和接听每个电话的等待时间(以秒为单位)的数据(持续时间)。您可以使用变异图来分析等待时间。
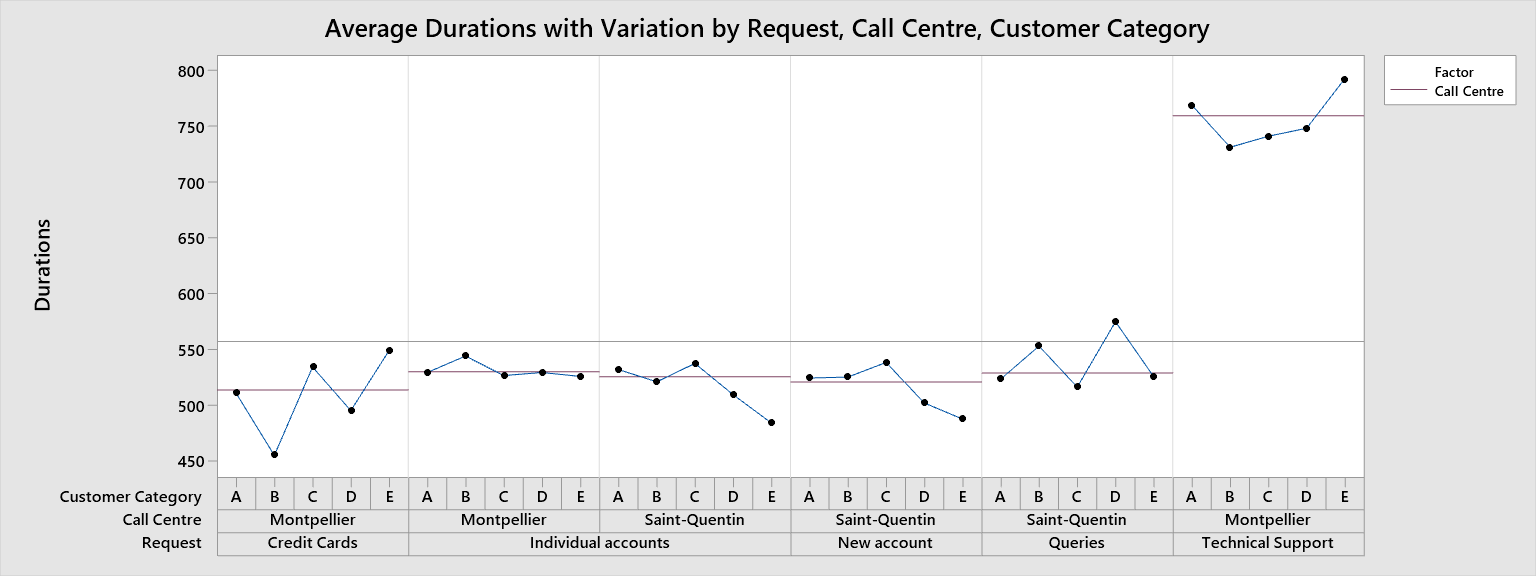
看看上面的可变性图表。显示呼叫中心、客户类别、等待时间和请求类型。每个呼叫中心都专门处理特定类型的请求。例如,技术支持电话仅在蒙彼利埃呼叫中心处理。
请注意右上角蒙彼利埃呼叫中心最长的持续时间是多少?如果查看 Minitab 项目中的其他图形,您也可以看到天数和小时数。他们表示,周一在蒙彼利埃的等待时间最长,而且蒙彼利埃每天的等待时间通常比圣康坦要长。周一的技术支持请求等待时间也更长。
但是,请注意,当没有明显的主导因素时,或者当来自过程的“信号”太“弱”而不易被检测到时,使用更强大的统计技术(例如ANOVA或回归分析)以数值估计每个因素的影响。
变异图之后的后续步骤
由于可变性图表中可变组件的出色可视化显示,金融服务公司可以轻松地看到技术支持电话和星期一是主要和明显的问题。现在公司可以采取下一步行动,开始调查存在这些问题的原因以及解决方法。 收起阅读 »
什么是变异图?
变异性图表是一种以可视化方式呈现方差分析 ( ANOVA ) 数据的好方法,它们在根本原因分析的早期阶段表现出色。它们的主要优势在于使您能够在单个图表中可视化许多不同的变化来源,同时提供因子效应的整体视图。
变异性图表可以帮助您在一张图表上进行调查和研究许多可能原因导致的变异模式。它们允许您显示过程中的位置或周期性变化。它们还可用于研究子组内、子组之间等的变异。
要在Minitab Statistical Software中创建变异性图表,请选择统计 > 质量工具 > 变异性图表... 然后在对话框中选择响应变量和最多八个因子。
使用变异图可视化呼叫中心等待时间
假设您需要检查来自一家大型金融服务公司的多个呼叫中心的等待时间。客户和潜在客户致电开立新账户、获取有关信用卡的信息、寻求技术支持和访问其他服务。您有关于客户类别、服务类型(请求)和接听每个电话的等待时间(以秒为单位)的数据(持续时间)。您可以使用变异图来分析等待时间。
看看上面的可变性图表。显示呼叫中心、客户类别、等待时间和请求类型。每个呼叫中心都专门处理特定类型的请求。例如,技术支持电话仅在蒙彼利埃呼叫中心处理。
请注意右上角蒙彼利埃呼叫中心最长的持续时间是多少?如果查看 Minitab 项目中的其他图形,您也可以看到天数和小时数。他们表示,周一在蒙彼利埃的等待时间最长,而且蒙彼利埃每天的等待时间通常比圣康坦要长。周一的技术支持请求等待时间也更长。
但是,请注意,当没有明显的主导因素时,或者当来自过程的“信号”太“弱”而不易被检测到时,使用更强大的统计技术(例如ANOVA或回归分析)以数值估计每个因素的影响。
变异图之后的后续步骤
由于可变性图表中可变组件的出色可视化显示,金融服务公司可以轻松地看到技术支持电话和星期一是主要和明显的问题。现在公司可以采取下一步行动,开始调查存在这些问题的原因以及解决方法。 收起阅读 »
劳斯莱斯黑带大师罗尔斯·罗伊斯关于数据驱动的卓越流程的黑带大师访谈的5个要点
Colin Noone透露,15年来,改进活动已经为罗尔斯·罗伊斯公司节省了26亿英镑. 凭借在发电工程公司40多年的经验,他热衷于与Minitab社区分享他的心得。
Colin是公司在方法和能力方面的全球黑带大师。下个月,他将在英国的Minitab Insights活动上发表演讲,这是我们为业务改善专业人士举办的全球系列会议的一部分。
在这段视频和采访中,我们请科林分享他对数据驱动的卓越和Minitab在劳斯莱斯的作用的看法,以及为什么他希望在Insights活动中遇到“志同道合的人”...
1.自上而下的领导,但赢得每个人的心和思想
今天,罗尔斯·罗伊斯公司是世界上第二大大型民用涡轮风扇发动机供应商。除了飞机发动机,罗尔斯·罗伊斯公司还生产火车、民用核能、海军和潜艇发动机——有些小到个人电脑,有些直径达116英寸。
(还有豪车?不,那是不同的劳斯莱斯;几十年前从工程公司分离出来的汽车品牌。)
亨利·莱斯是该公司的联合创始人,他有一句名言:
高层对质量的这种要求使得该公司的产品如此受欢迎,以至于它的名字成了英国语言中“最高质量”的代名词。
这让我们很好地理解了科林关于最佳方法的第一条建议:
真正确保你从领导开始,从高层开始推动。必须有一个清晰的愿景。
但是,这不应该以牺牲操作流程的人员的参与为代价:
如果你不与人民接触,领导说什么都不重要,不会有所作为。因此,赢得人心,赢得人民的力量,对于任何想要改善的组织来说都是至关重要的。
2.在“有所作为”中以身作则
作为罗尔斯·罗伊斯的黑带大师,科林负责全球范围内的精益六适马黑带(黄带、绿带、黑带、黑带大师)的培训和认证计划。
卓越流程、卓越运营、业务改进和持续改进的名称...对科林来说,它们都是一回事。
这是为了在组织中有所作为。你叫它什么真的不重要。重要的是你实际做了什么。
Colin建议您以身作则,“传达这样的信息:改变是好的,改变是积极的事情,通过合作,我们绝对可以改善组织的运营方式”。
任何一个在组织中从事职业改进的人都应该以身作则。“向人们展示方法,使用教练风格来帮助提高人们对如何应用过程改进工具和技术的理解。”
我认为,有了那种想要有所作为的激情和动力,你就可以带领整个组织前进,永远不会失去这种激情,如果你失去了这种激情,事情就会停滞不前。
3.关注真正发生的事情和你的数据告诉你的事情
科林建议说,“虽然流程被写了下来,这是它们应该如何操作,但现实世界通常是不同的,理解流程实际上在做什么是关键。”
在唾手可得的果实之后,寻找“真正的机会,从根本上改变一些大的有问题的过程,这些过程可以对一个组织的运作方式产生根本的影响”。
任何组织都应该问自己这样一个问题,我们是否尽了最大努力?我们是否尽了最大努力?我们是否从根本上及时满足了客户的需求?
如果没有,我们需要做些什么。这就是我认为数据可以真正帮助你理解组织中正在发生的事情的地方。'
这看起来说起来容易做起来难。科林说:“对于任何改进活动,当然是较大的组织,他们不缺少的一样东西就是数据。”。
真正的问题是理解这些数据告诉你什么。我不认为为了数据而收集数据会给组织增加价值。
它是关于收集正确的数据,理解它告诉你什么,并使用这些数据做出明智的决策,以推动组织内问题的解决和改进。
4.分析您的数据是一项战略性投资
15年来,罗尔斯·罗伊斯公司的改进活动已经节省了26亿英镑。罗尔斯·罗伊斯一直是Minitab的客户:
我们已经与Minitab合作了16年,我认为Minitab在未来许多年都将是一个真正的战略合作伙伴。
“Minitab帮助我们分析数据的能力对劳斯莱斯来说至关重要,因为我们正在进入一个数据变得越来越容易获得的世界,我认为就如何分析和理解数据而言,数据湖是一个挑战,Minitab是关键所在。”
劳斯莱斯的每个部门都可以使用精益六适马培训和Minitab。科林说,这不仅仅是制造工艺的改进。
5.结识您的同行并分享您的见解
尽管Colin将于下个月在英国的Minitab Insights活动上分享一个新的演示文稿,并于去年在我们在爱尔兰的活动上发言,但他不仅仅是为了站在舞台上。
我想参加Insights活动的原因,不仅仅是想成为一名演讲者。这是为了结识志同道合的人,他们也试图在自己的业务中有所作为,分享经验,什么是有效的,什么是良好的做法,并分享经验,我们所面临的挑战。然后,我们应该能够将这种共享的学习成果应用到我们自己的组织中,并取得良好的效果。
Colin推荐Insights活动为“一个很好的基准机会”...“我们在我们所做的事情上相当成熟,我们显然可以做得更好,但我会看看其他代表并与他们交谈,以了解他们一直在做什么,如果我能从他们那里学到什么,我们可以在劳斯莱斯内部应用,以在未来产生影响。”
收起阅读 »
Colin是公司在方法和能力方面的全球黑带大师。下个月,他将在英国的Minitab Insights活动上发表演讲,这是我们为业务改善专业人士举办的全球系列会议的一部分。
在这段视频和采访中,我们请科林分享他对数据驱动的卓越和Minitab在劳斯莱斯的作用的看法,以及为什么他希望在Insights活动中遇到“志同道合的人”...
1.自上而下的领导,但赢得每个人的心和思想
今天,罗尔斯·罗伊斯公司是世界上第二大大型民用涡轮风扇发动机供应商。除了飞机发动机,罗尔斯·罗伊斯公司还生产火车、民用核能、海军和潜艇发动机——有些小到个人电脑,有些直径达116英寸。
(还有豪车?不,那是不同的劳斯莱斯;几十年前从工程公司分离出来的汽车品牌。)
亨利·莱斯是该公司的联合创始人,他有一句名言:
高层对质量的这种要求使得该公司的产品如此受欢迎,以至于它的名字成了英国语言中“最高质量”的代名词。
这让我们很好地理解了科林关于最佳方法的第一条建议:
真正确保你从领导开始,从高层开始推动。必须有一个清晰的愿景。
但是,这不应该以牺牲操作流程的人员的参与为代价:
如果你不与人民接触,领导说什么都不重要,不会有所作为。因此,赢得人心,赢得人民的力量,对于任何想要改善的组织来说都是至关重要的。
2.在“有所作为”中以身作则
作为罗尔斯·罗伊斯的黑带大师,科林负责全球范围内的精益六适马黑带(黄带、绿带、黑带、黑带大师)的培训和认证计划。
卓越流程、卓越运营、业务改进和持续改进的名称...对科林来说,它们都是一回事。
这是为了在组织中有所作为。你叫它什么真的不重要。重要的是你实际做了什么。
Colin建议您以身作则,“传达这样的信息:改变是好的,改变是积极的事情,通过合作,我们绝对可以改善组织的运营方式”。
任何一个在组织中从事职业改进的人都应该以身作则。“向人们展示方法,使用教练风格来帮助提高人们对如何应用过程改进工具和技术的理解。”
我认为,有了那种想要有所作为的激情和动力,你就可以带领整个组织前进,永远不会失去这种激情,如果你失去了这种激情,事情就会停滞不前。
3.关注真正发生的事情和你的数据告诉你的事情
科林建议说,“虽然流程被写了下来,这是它们应该如何操作,但现实世界通常是不同的,理解流程实际上在做什么是关键。”
在唾手可得的果实之后,寻找“真正的机会,从根本上改变一些大的有问题的过程,这些过程可以对一个组织的运作方式产生根本的影响”。
任何组织都应该问自己这样一个问题,我们是否尽了最大努力?我们是否尽了最大努力?我们是否从根本上及时满足了客户的需求?
如果没有,我们需要做些什么。这就是我认为数据可以真正帮助你理解组织中正在发生的事情的地方。'
这看起来说起来容易做起来难。科林说:“对于任何改进活动,当然是较大的组织,他们不缺少的一样东西就是数据。”。
真正的问题是理解这些数据告诉你什么。我不认为为了数据而收集数据会给组织增加价值。
它是关于收集正确的数据,理解它告诉你什么,并使用这些数据做出明智的决策,以推动组织内问题的解决和改进。
4.分析您的数据是一项战略性投资
15年来,罗尔斯·罗伊斯公司的改进活动已经节省了26亿英镑。罗尔斯·罗伊斯一直是Minitab的客户:
我们已经与Minitab合作了16年,我认为Minitab在未来许多年都将是一个真正的战略合作伙伴。
“Minitab帮助我们分析数据的能力对劳斯莱斯来说至关重要,因为我们正在进入一个数据变得越来越容易获得的世界,我认为就如何分析和理解数据而言,数据湖是一个挑战,Minitab是关键所在。”
劳斯莱斯的每个部门都可以使用精益六适马培训和Minitab。科林说,这不仅仅是制造工艺的改进。
5.结识您的同行并分享您的见解
尽管Colin将于下个月在英国的Minitab Insights活动上分享一个新的演示文稿,并于去年在我们在爱尔兰的活动上发言,但他不仅仅是为了站在舞台上。
我想参加Insights活动的原因,不仅仅是想成为一名演讲者。这是为了结识志同道合的人,他们也试图在自己的业务中有所作为,分享经验,什么是有效的,什么是良好的做法,并分享经验,我们所面临的挑战。然后,我们应该能够将这种共享的学习成果应用到我们自己的组织中,并取得良好的效果。
Colin推荐Insights活动为“一个很好的基准机会”...“我们在我们所做的事情上相当成熟,我们显然可以做得更好,但我会看看其他代表并与他们交谈,以了解他们一直在做什么,如果我能从他们那里学到什么,我们可以在劳斯莱斯内部应用,以在未来产生影响。”
收起阅读 »
Minitab使绘制直方图比Excel更加自动化和简单的3种方法
直方图对于汇总几个统计数据非常有用。但是,无论您是否启用了数据分析工具库,或者您是否正在打造一条公式之路(计数、平均值和标准差,天啊!),在Excel中创建直方图并不总是那么好。我们开发了Minitab统计软件,成为您的直方图制作工具。
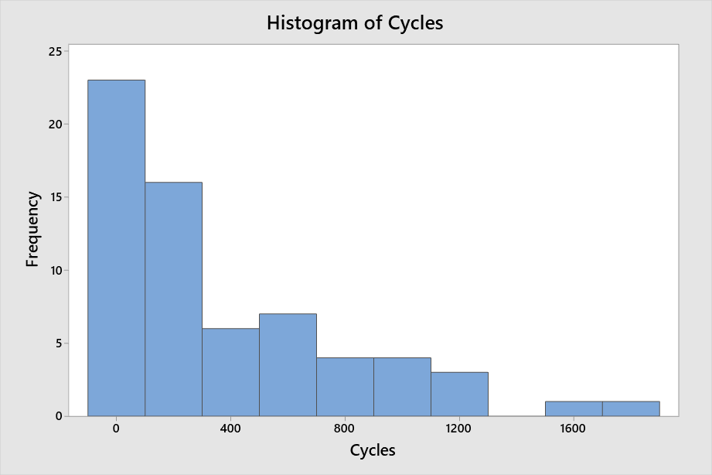
让我们看看在Minitab中使用直方图的三种方法。对于第一个问题,我们将使用一个洗碗机喷淋臂可靠性的例子。您可以下载数据集如果你想继续的话。
1.对于您的BIN范围,您只需要两个数字
垃圾箱用于对样本数据进行排序的等距区间。在直方图中,它们显示为条形。一旦你输入你的数据,Minitab会遵循一个算法,生成一个非常好的标准直方图。这并不意味着您不想探索一下,看看小的变化是否会影响直方图的外观。下面是我们洗碗机喷淋臂可靠性数据集的简单直方图:
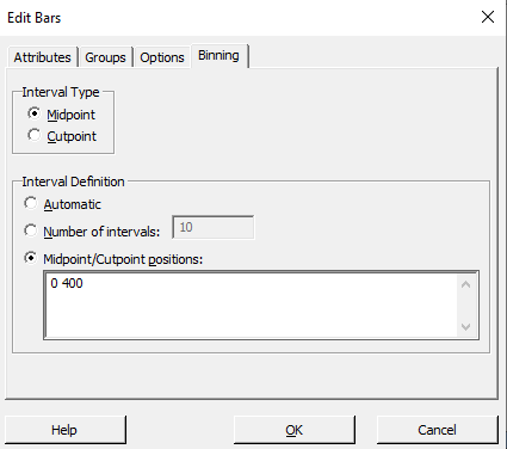
要轻松重新定义媒体夹:
双击图表和编辑图表窗口将会打开。
双击其中一个条。
挑选扔掉.
挑选中点/切割点位置.
在…里中点/切割点位置输入2个连续的中点或输入定义数据的单个bin的值。点击好.
“输入两个值?”你可能会说“但是我更喜欢在我的图上有五个箱子!”
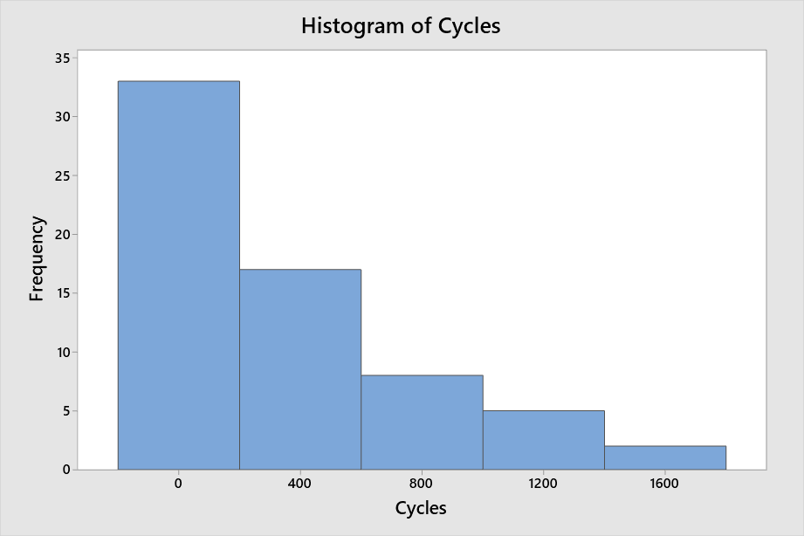
Minitab让这一切变得简单。当您输入两个值时,Minitab会扩展容器的范围,以包含您的其余数据。所以如果你输入的只是两个数字…
…然后Minitab会为您完成剩下的工作:
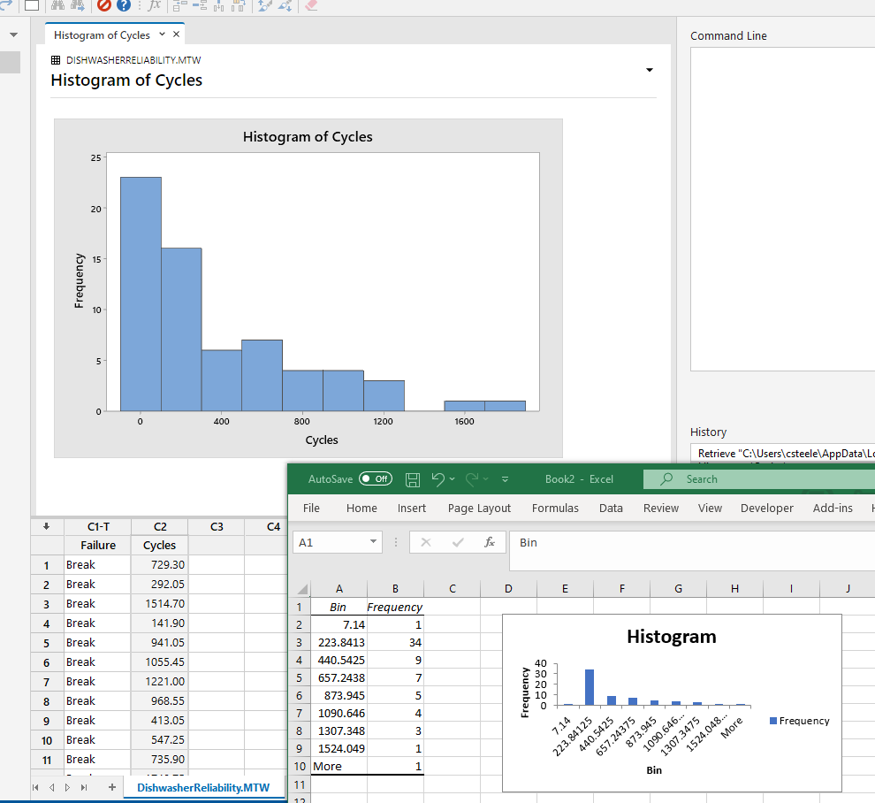
在Excel中制作直方图相对容易,但使用这种数据集,Y轴范围非常狭窄,图形最终太小,不够清晰,无法阅读和理解。
它看起来也不精致,除了bin范围不能自动为您处理之外,您还会遇到一些bin范围的问题。
如果条柱范围不明确,您将无法确定它们是否代表相同的距离量级,而这对于正确评估数据的分布和形状至关重要。
除非你已经定义了所有的箱子,否则Excel会在末尾加上一个名为“更多”的箱子,把所有的东西都放在一起。这个“多”让我们无法判断价值观相差有多远。即使将最大值从1740.75更改为999999999,也会得到具有完全相同的条柱的完全相同的直方图。
2.您可以使用MINITAB助手制作易于比较的直方图
现在你知道直方图使分析单个数据样本的特征变得多么容易了。但是你知道吗,它们也非常适合用来比较样品?
您可以通过以下方式实现这一切Minitab的助手。为此,我们将使用库中的另一个数据集,盖子拆卸扭矩数据。下载并打开Minitab文件,然后按照这些说明进行操作。
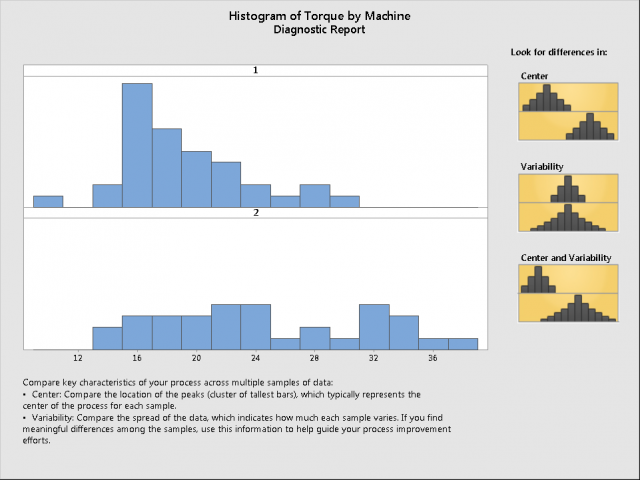
选择助手>图形分析
点击柱状图
在…里y列,输入转矩.
在…里x列,输入机器。点击好.
您只是将获得易于比较的直方图所需的步骤减少了一半。直方图的排列方式不仅便于比较,而且助手的诊断报告还会提醒您可以看到的一些重要差异。数据是否有相同的中心?数据是否具有相同的可变性?中心和可变性是否都不同?在这种情况下,看起来中心和可变性在组之间都不同。
3.您可以从记录的数据中创建直方图。
总有一天,有人会给你他们记录的数据,而不是你习惯使用的漂亮的单个数字列。想象一下,如果你愿意,它会像这样放在你的桌子上:
一个不太重要的人可能会感到害怕和厌恶。那些数据里有超过300个数字。但不是你。你很擅长Minitab,你知道你不需要输入超过300个数字。您可以直接使用这些数据。首先,将数据输入Minitab
然后,按照以下步骤操作:
选择图表>直方图
选择简单的。点击好.
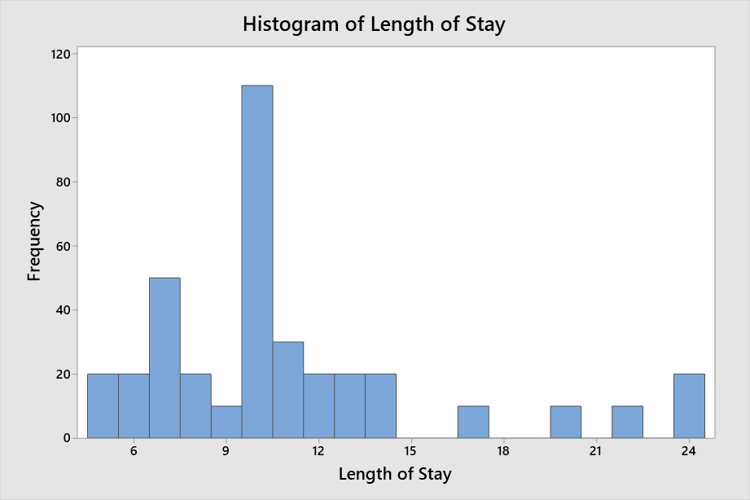
在…里图形变量,输入停留时间.
点击数据选项.
点击频率.
在…里频率变量,输入频率.
点击好两次。
你会得到这个直方图:
请记住,如果你想改变周围的垃圾箱,你可以只使用两个数字,Minitab会照顾其余的!
总结
无论您想要快速浏览不同的条柱,在直方图之间进行比较,还是根据计数制作直方图,Minitab都能让您轻松快捷。直方图中包含了您在如何改进流程方面做出正确决策所需的全部信息。现在您知道如何在Minitab中更好地利用直方图了。 收起阅读 »