实验设计中如何判因子之间的断嵌套与交叉问题

是交叉还是嵌套 （引用百度文库资料整理）
 
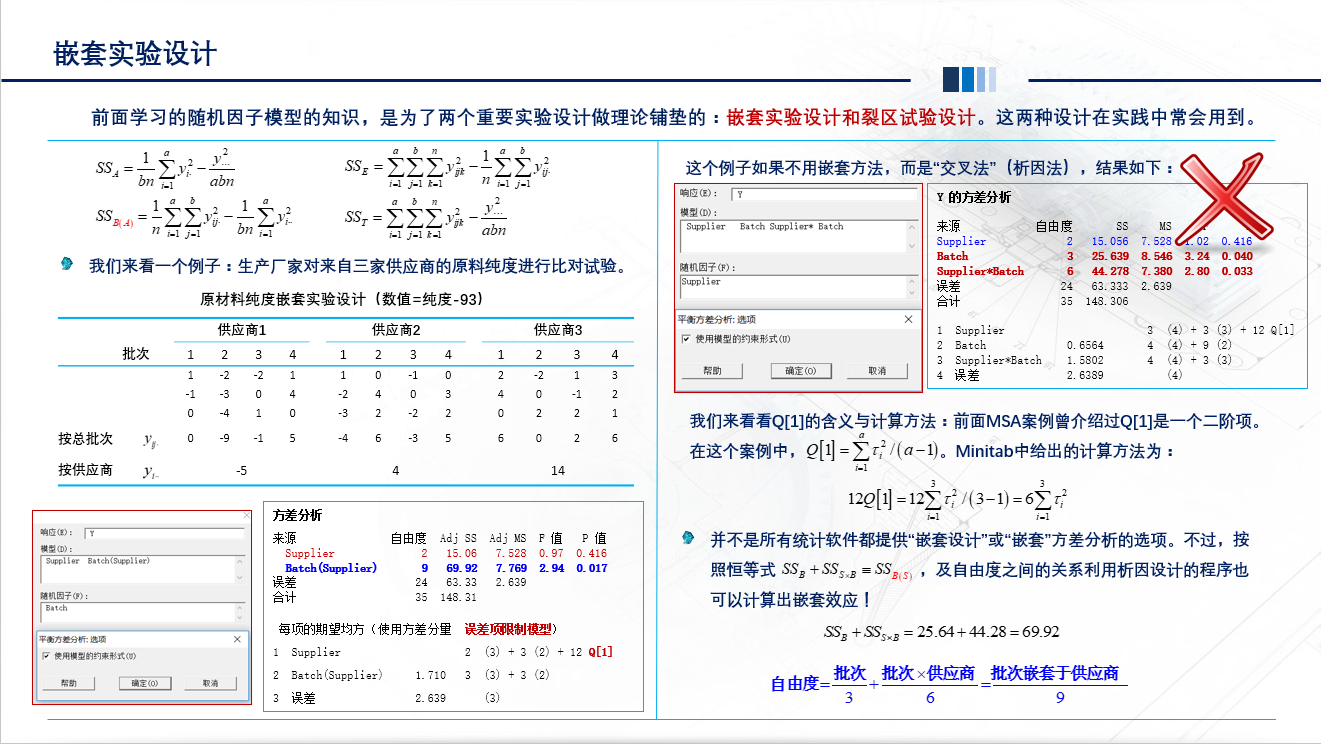
例子一：考虑车工车间在生产标准螺钉时的直径波动过大问题。
 
随机选取3 名工人，各自分别加工出4 颗螺钉，然后在每颗螺钉的根部随机选取两个相互垂直的方向，分别测量其直径，共得到24 颗数据。将"工人"这个因子记为因子A ，将 "螺钉" 这个因子记为因子 B ，那么， A 与 B 两个因子间是什么样的关系呢?
 
由于每个工人生产的4 颗螺钉，是分别附属于相应的工人的。 即使我们将这些螺钉都编号为 1 ， 2 ， 3 ， 4 ，但是很明显，工人A 和工人B 之下的编号皆为1 的两颗螺钉并不是同一件东西。这时，称因子B "螺钉"是被因子A"工人"所嵌套着的 (Factor B is nested with factor A) 。很明显，此种情况下的两个因子所处的地位是不能被颠倒过来的。
 
然而，在实际情况中，两个因子间还可能存在另一种关系。例如，3 名工人轮流使用共同的4 台编了号的车床，每个工人都使用了车床 1， 2 ， 3 ， 4 ，这时，工人A 和工人B 之下的编号都为 1 的两台车床是同一件东西。 而且可以反过来说，每台车床都被3 名工人使用过。这时，称因子B "车床"是与因子A "工人"相交叉 (Factor B is crossed with factor A) 。很明显，如果这时  候说因子A"工人"与因子B "车床"相交叉也是同样的，它们的位置是可以颠倒过来的。这里要注意，单从树状图上是不能区分两个因子的关系是交叉还是嵌套的，只能从实际意义判断之。
 
例子二：选取3 名工人，让他们使用编好号的 4 台车床，按随机顺序各自分别加工出 3 根立轴。
 
若将与因子A (工人) 及搭配的因子B ( 车床) 的每台车床编好号，则可以发现，因子A (工人)与因子B (车床) 间的关系是交叉关系。 注意，它们两因子间可以颠倒顺序，即可以反过来说，因子B (车床) 的每个值也都与因 子A (工人) 的每个值搭配过。
 
如果车床不是固定的编号的车床，而是每个工人各自有自己固有的4 台车床，这时因子A (工人)与因子 B(车床) 间的关系就不再是交叉关系，而是嵌套关系了。  
 
例子三： 现在讨论三因子问题。由于不能将立轴（半成品尺寸/材质等等）之间的变异看成随机误差，因而要求将立轴之间的变异也看成因子，即形成三因子问题。这里3 名工人 (因子A) ，分别使用己选好并编了号的4 台车床(因子B)，各自分别加工出3 根立轴 (因子C)，然后对每根" 立轴测两次直径(误差)。由于因子B 的4 台车床是固定的，所以工人(因子A) 与车床 (因子B) 之间是交叉关系，而立轴 (因子C) 则是被A 与B 所嵌套的，即三因子是先交叉后嵌套的关系。
 
如果，将例子10-3 的安排稍加调整： 3 名工人 (因子A) ，分别使用自己固定的4 台车床(因子B)，各自分别加工出3 根立轴 (因子C)。，这时因子间的关系就会发生变化。这时B被A 所嵌套， C 被A，B 所嵌套，这种关系也被称为全嵌套关系 (fully nested) 。 
 
实际问题中可能有多种结构，但仔细分析它们的数据就可以发现，因子间的关系无非 是嵌套或交叉这两种基本类型。有时在实际问题中可能遇到的是因子个数较多，关系较复杂，这时需要仔细分析处理。