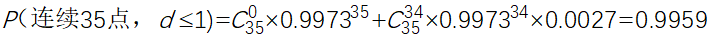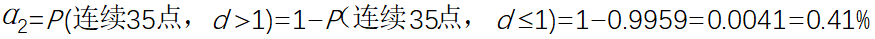SPC控制图的判异与判稳

学习过SPC的朋友大都熟悉常规控制图的8大判异准则，这些判异准则详见我的前一篇文章“借助于PFMEA选择控制图判异准则”。控制图的判异是基于统计学中的“显著性检验”，例如，判异准则1——1个点，距离中心线超过3个标准差，也就是说，当过程受控时，只有0.27%的概率超过3个标准差，即I类错误（将受控误判为失控）的概率α=0.27%，是小概率事件，若真的超过了，就说明过程真的失控了。反过来讲，如果这一个点位于3个标准差之内，就可以说过程稳定受控吗？这样讲对吗？

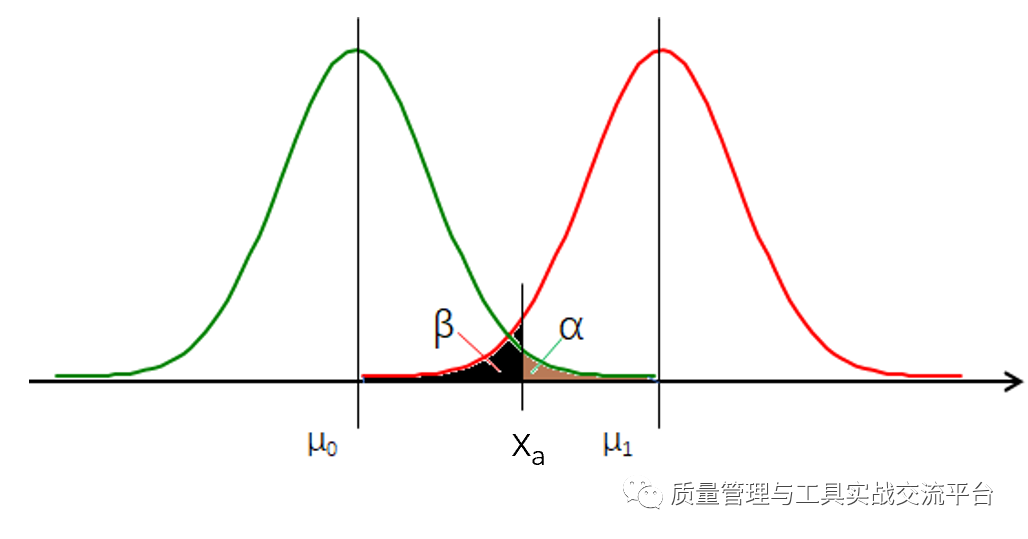
从统计学上来讲，如是I类错误α的概率很小，则II类错误（将失控误判为受控）β的概率将很大，如下图所示，左边的绿色分布图代表着受控时点的概率分布，右边的红色分布图代表着失控时点的概率分布，Xa是临界点，相当于控制图的控制限，如果Xa向右移，则α将会变小，而β将会变大。因此，如果是只用1个点在正负3倍标准差范围内作为判断过程受控的基准，这将会有过高的II类错误的风险。


故，我们不能只使用1个点来判断过程是否受控，但可以使用多个连续的点来进行判断，这是因为多个，例如n个连续的点在一起的II类风险概率将是βn，基于这个理论，规定了以下3个判稳准则，符合任何一个，就可以认为过程受控：

（1）连续25个点子都在控制界限内；
（2）连续35个点子至多1个点子落在控制界限外；
（3）连续100个点子至多2个点子落在控制界限外。

我们分别计算一下这3条准则的α：

对于准则2：当过程受控的时候，连续35个点中，至多1个点落在控制界限外的概率为：


故

也就是说，如果使用判稳准则2，则只有0.41%的概率将受控误判为失控，这与判异准则1中的0.27%处于同一个数量级上。

同样的方法，我们还可以得到判稳准则1和3的α：

α1=6.54%，α3=0.26%，

其中，准则1的I类风险还是比较高的，因此，有的专家认为可以不使用准则1。

可见这3条准则的I类风险是依次递减的，但这3条准则所需要的样本数量是依次递增的，成本也是递增的。为此，可以按照下列程序来使用：

使用判稳准则1，若不能判稳，则使用准则2；
使用判稳准则2，若还不能判稳，则使用准则3；

使用判稳准则3，仍不能判稳，则应停止使用判稳准则。

当出现界外点时，我们必须调查原因，确认是特殊原因造成的，还是属于I类错误，如果是特殊原因造成的，则应对过程进行改进，使其回到稳态。

现在，我们已经学习了判异准则和判稳准则，接下来的问题是：什么时候使用判稳准则，什么时候使用判异准则呢？

判稳准则，就是用来判断过程是否是稳定受控的，这正好适用于控制图的第一阶段——分析阶段控制图。控制图的分析阶段的任务是通过有限的样本建立控制限，而控制限在用于第二阶段——控制阶段之前，必须满足2个条件：1）过程必须是稳定的；2）过程的能力是足够的。一般情况下，是通过抽取25个子组，即通过25点来建立控制限的，因此我们可以先使用判稳准则1——连续25个点没有超过控制限，来判断过程是否稳定。当然 ，为了更加有信心，我们可以使用准则2或者准则3。

在控制图的正式使用的过程中（控制阶段），我们首先使用判异准则1，若发现有1点超限，则有两种可能：1）存在特殊原因；2）属于判异准则1的α错误。在调查原因后，如果没有发现特殊原因，我们就可以从那个超限的点开始，再使用判稳准则来判断过程是否真的没有失控。

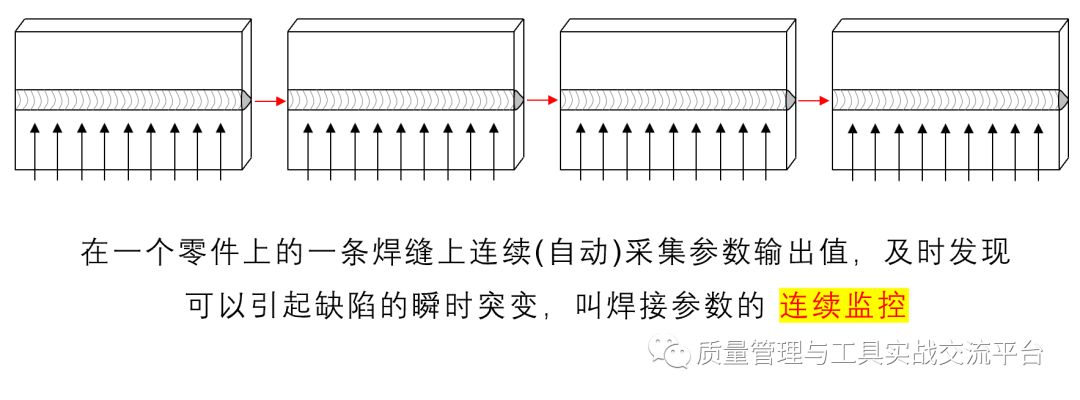
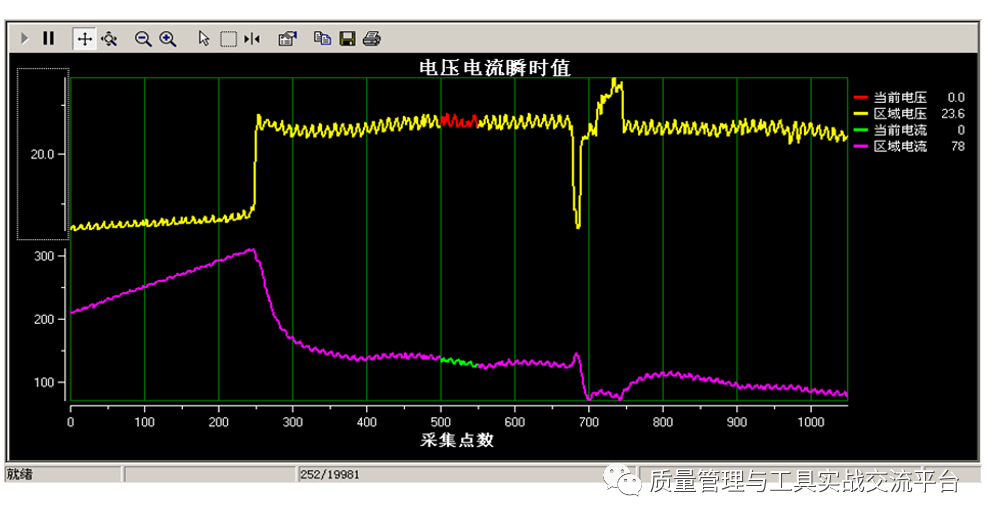
当然，出现超限点而找不到原因，也会存在这样的一种可能：过程出现了NTF原因，即不能够再现的原因，只是偶尔出现过一次，随后又恢复了正常，当我们去调查时，一切正常，不留任何痕迹。对于这种类型的问题，依赖于周期性抽样的控制图就不适用了！我们应当导入连续采样系统，与零件的序列号关联，进行连续监控、实时报警和追溯。这种系统的采样周期是很短的，如焊接电流的输出采样，采样周期可达几十毫秒，这属于大数据控制的范畴了，如下图所示。