控制图为什么能够发现失控?

假设你是一位质量工程师，在使用SPC控制图控制你们的生产过程。某一天，当你发现控制图失控的时候，你要求停线调查原因、隔离产品，那么你很可能将遭受到来自生产部门和销售部门的质疑和压力：你凭什么让我们停线？你凭什么不让我们交付？你凭什么说超过了那两条控制限过程就有问题？

这时你就需要拿出你掌握的底层逻辑，即控制图的理论依据来了，否则，就不能说服他们。


我们先来看一下控制图的第一条判异准则：当有一点超过中心线上、下3个标准差的控制限。

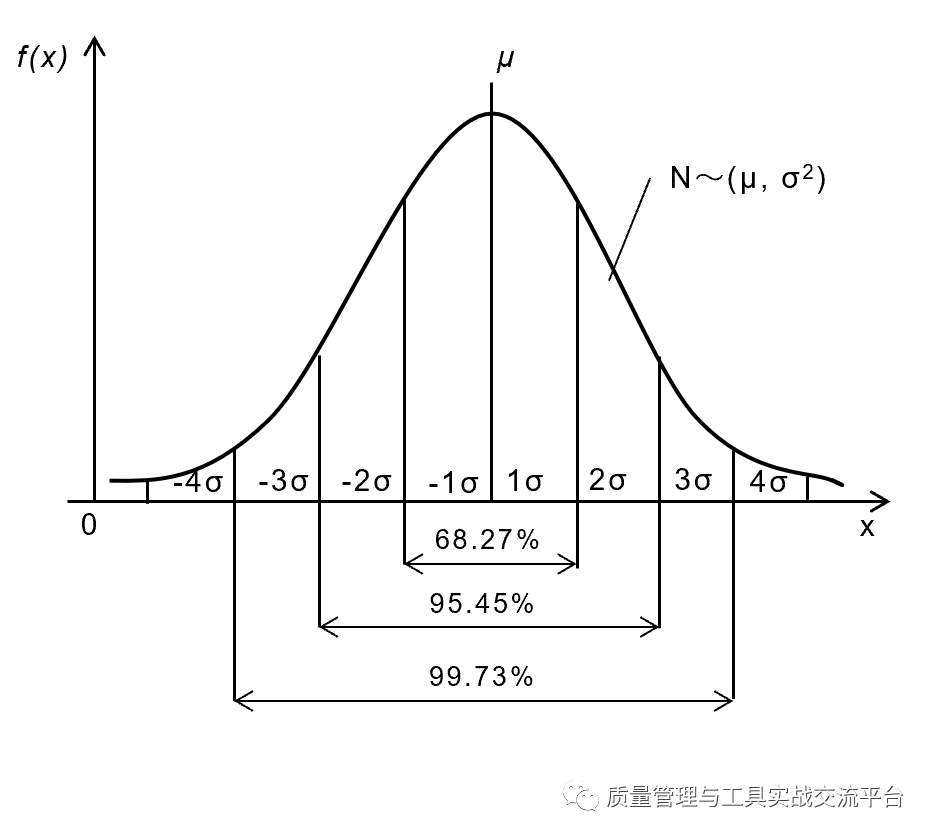
在绝大多数制造过程中，如果特性值的影响因素有若干，且没有一个是起主导作用的，这些特性数据就会符合或者大致符合正态分布，这是一个经过大量实践证明了的客观规律，如下图所示，它是一个概率分布图。正态分布中，位于均值μ两侧各3个σ以外的概率为（1-99.73%)=0.27%。


 
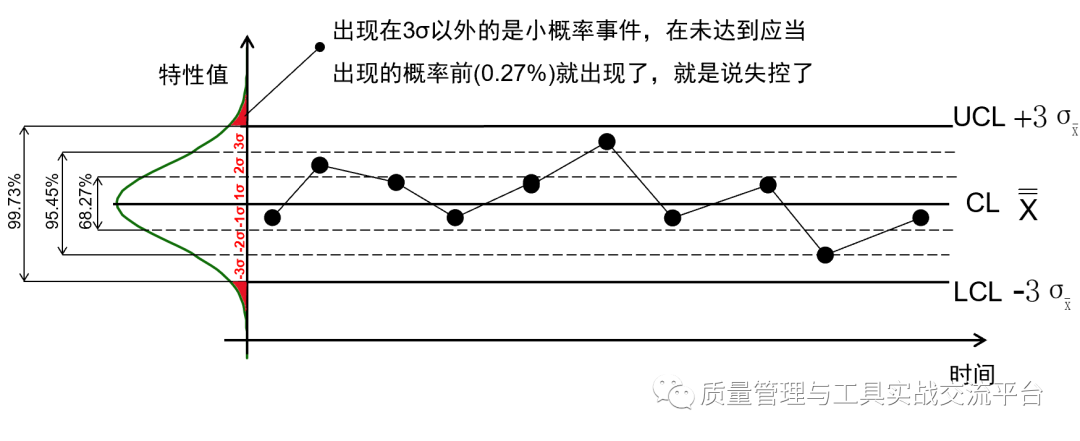
在常规控制图的均值-极差控制图中，以中心线上、下3倍子组均值标准差为均值图的上、下控制限，如下图所示。均值图中的点代表子组的均值，根据中心极限定理，它们之间也符合正态分布，而且会比单值更加符合。根据正态分布的规律可知，在过程稳定受控（也叫统计受控）的状态下，出现一个数据点超过控制限的概率仅为0.27%，反之，如果出现的概率超过0.27%，则说明该生产过程不稳定，即失控。



换种说法就是，如果过程稳定受控，平均1/0.0027≈370个点中才有一个点超出控制限，这是一个妥妥的小概率事件！小概率事件的发生概率很小，它在一次试验中是几乎不可能发生的，但在多次重复试验中是必然发生的，在这里的“多次”，就是370次以上。那么，一旦我们真的发现有点超过了控制限，首先应当问：上次有点超过控制限到这一次，是经历了多久？如果两次相隔达不到370个点以上，那么就说明过程已经失控了。

在未达到小概率事件出现的机会之前就出现了，说明过程原来的稳定状态已经被一种起主导作用的原因破坏了，这个原因叫做特殊原因，我们应当停下生产线来找到这个原因，否则就会出现批量的不良品。

我们近些年中每年动不动就会遭遇百年不遇的暴雨、洪灾、干旱，而百年不遇本来就是一个小概率，为什么近几年每年都会发生呢？这是因为存在了特殊原因，使得我们这个星球上的大气系统变得不再稳定，这个特殊原因就是气候变暖！类似的社会生活中的例子可以举出很多。



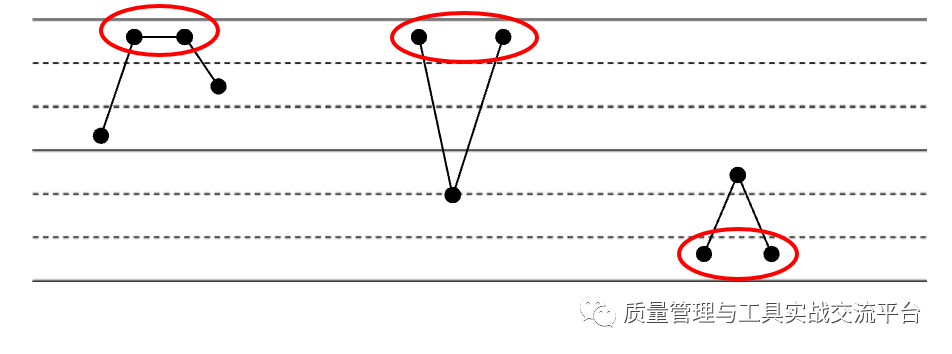
我们再看一下准则5：连续3个点中，有2个位于中心线同侧2倍标准差以外。


 
按照正态分布的概率密度分布规律，一个点出现在中心线一侧2标准差以外的概率为:P(X>μ+2σ)=1-P(X≤μ+2σ)=1-0.9772=0.0228，P(X<μ-2σ)=0.0228，则连续3个点中有2个点位于中心线同侧2标准差以外的概率应：



这更是一个小概率事件！

总之，在常规控制图中，我们基于大多数稳定的制造过程数据符合或接近正态分布这一客观规律，做一个过程稳定的假设，即过程数据符合正态分布，一旦出现不符合正态分布的情况，我们就判定这个过程失控了，就必须停止生产，找出导致失控的特殊原因。

这就是为什么控制图能够发现失控的底层逻辑，即它的理论基础。