1分钟教你制作双比例检验

作为公司的采购经理，您需要授权采购二十台新复印机。在根据价格、复印质量、保修和功能对多个品牌进行比较后，将选择范围缩小到两个品牌：X 品牌和 Y 品牌。您认为决定性因素是品牌的可靠度，定义为在购买后一年内需要维修的比率。

由于您的公司已经使用过这两种品牌，因此可获得每种品牌随机选择的 50 台机器的维修历史记录信息。记录显示，六台 X 品牌的机器和八台 Y 品牌的机器需要维修。使用此信息可以指导您选择要购买的品牌。
 
操作:
1, 6SQ统计--估计和假设检验--双比例检验

 
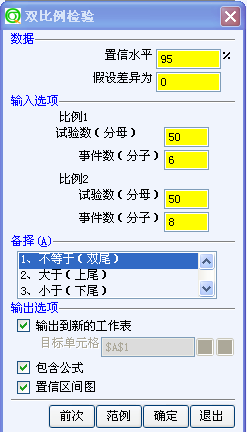
2， 比例1 分母输入 50  事件数输入 6  
    比例2 分母输入 50  事件数输入 8
 备择假设选择  不等于


 
3, 确认输出结果




解释结果

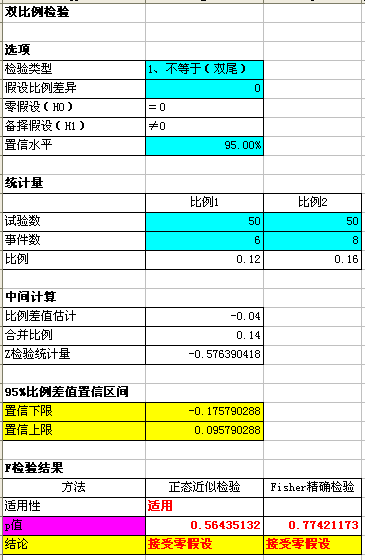
对于此示例，正态近似检验有效，因为对于两个样本而言，事件数都大于四，试验数与事件数之间的差值也大于四。正态近似检验报告 p 值 为 0.564，Fisher 精确检验 报告 p 值为 0.774。这两个 p 值都大于通常选择的 a 水平 。因此，数据与总体比率相等的原假设一致。换句话说，在第一年内需要维修的复印机比率不因品牌不同而存在差异。作为采购经理，您需要根据别的标准来决定采购哪种品牌的复印机。

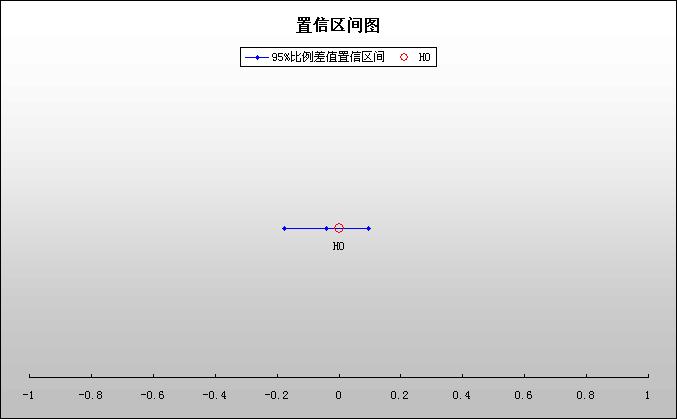
由于正态分布有效，因此从 95% 置信区间 中可以得出相同的结论。由于零位于置信区间（-0.0957903 至 0.175790）之内，因此可以得出结论，数据与原假设一致。如果您认为置信区间太宽，并且未提供有关 p1-p2值的精确信息，则可能需要收集更多数据才能获得差值的更好估计。
 
Excel案例数据
http://pan.baidu.com/s/1i5AXSRN​
6SQ统计3.0企业版90天试用下载​ http://pan.baidu.com/s/1i5AXSRN