MINITAB 之弹指神通--利用缺失数据进行实验设计的成功案例
MINITAB 15 之弹指神通
-- 利用缺失数据进行实验设计的成功一例
上海先进半导体制造股份有限公司 6Sigma经理 高级工程师 闵亚能
内 容 提 要
通过获得最佳的焊缝渗透的工艺参数的实验设计,剖析了由于缺失数据的存在,造成了正交性与平衡性的失拟,导致了因子的效应不能独立预估,并降低了模型的精确度。通过对失拟的程度评判作出决策,如果稍有一些失拟,影响也比较小,但是,如果随着缺失数据的增加,失拟也在增大。针对多数情况,还是可以通过功能强大的MINITAB的菜单操作能够轻易完成的。本实验的成功应用到实际工作中,开创了解决异常问题的复杂实验设计的新局面。
实验设计 缺失数据分析 实验精确度
概述
什么是实验设计中的缺失数据?
如果一个或多个实验处理没有响应值,那么DOE的分析涉及到缺失数据的分析。
什么时候在设计的实验中会发生缺失数据?
有好几种情况导致不完全的实验设计的发生,形成了实验中的缺失数据:
 实验被停止,因为完成实验所需要的资源不再提供,如没有时间、资金、原材料等。
 从实验中获得的数据不正确的,在残差分析中出现明显的奇异数据。观察到的奇异数据,常常是由于测量错误,数据登录错误,不寻常的环境条件,和实验设置的问题。
 观察到的数据丢失了。
在实验设计中怎样分析缺失数据?
你可以使用 MINITAB 的DOE 菜单来分析,虽然设计一般不再正交,但是,我们通过评估缺失数据对模型的影响程度,利用逐步回归进行分析,在减少模型时,一次减少一个因子的方法,最后得到简化的适合模型。
问题的由来
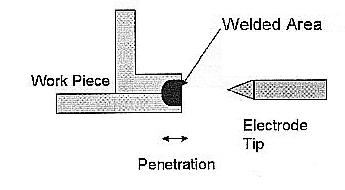
一种钨(惰性气体)焊接操作是在二块钢板之间产生一条焊缝,焊缝渗透深度会影响装配件的使用寿命。期望获得较大的焊缝渗透深度,制造厂购买了一种新的焊接设备。 工程师进行试验来找出以获得最佳的焊缝渗透深度的工艺设计参数。
焊接工艺关键的可控制的变量是:
火把/电极速度(Speed),焊接电流(Current),气体流动速度(Flow)和工件到焊接点的距离(Distance)。这些因子有些在实际应用中有交互作用,因此工程师们创建了一个全因子设计来考虑和估计交互作用。他们复制了一个全因子实验设计,以获得更好的因子主效应与交互作用的效应估计。
数据收集
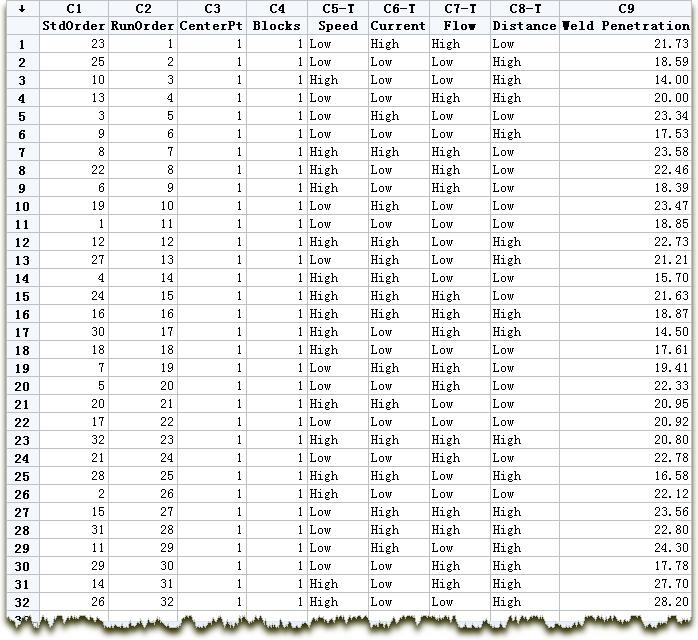
数据文件Missingdata.MPJ
变量 描述
StdOrder 标准序
RunOrder 运行序
CenterPt 中心点
Block 区组
速度(Speed) 电极速度
焊接电流(Current) 焊接电流
流速(Flow) 气体流速
距离(Distance) 工件和电极尖端的距离
焊缝渗透深度(Weld Penetration) 二块钢板的焊缝深度
分析步骤
 阶段 1 : 制定完全模型(Full model)的 ANOVA表,解释结果
1) 打开文件 MISSINGDATA.MPJ
2) 选择 统计 > DOE > 因子 > 分析因子设计
3) 在响应栏选择 Weld Penetration(焊缝渗透深度)
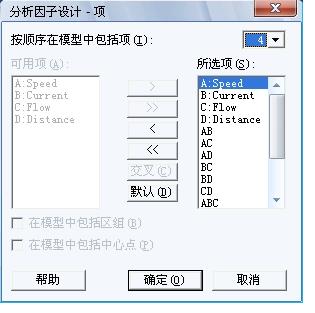
4) 点击 项
5) 完成如下对话框
6) 点击 确定
结果分析
拟合因子: Weld Penetration 与 Speed, Current, Flow, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 20.7631 0.7069 29.37 0.000
Speed -0.7988 -0.3994 0.7069 -0.56 0.580
Current 1.0563 0.5281 0.7069 0.75 0.466
Flow 0.7637 0.3819 0.7069 0.54 0.597
Distance -0.3825 -0.1912 0.7069 -0.27 0.790
Speed*Current -1.5738 -0.7869 0.7069 -1.11 0.282
Speed*Flow 0.4912 0.2456 0.7069 0.35 0.733
Speed*Distance 0.5000 0.2500 0.7069 0.35 0.728
Current*Flow -0.2512 -0.1256 0.7069 -0.18 0.861
Current*Distance 0.5125 0.2563 0.7069 0.36 0.722
Flow*Distance -0.4050 -0.2025 0.7069 -0.29 0.778
SpeedCurrentFlow 1.2263 0.6131 0.7069 0.87 0.399
SpeedCurrentDistance -1.3500 -0.6750 0.7069 -0.95 0.354
SpeedFlowDistance -0.7600 -0.3800 0.7069 -0.54 0.598
CurrentFlowDistance 0.1950 0.0975 0.7069 0.14 0.892
SpeedCurrentFlow*Distance -1.0800 -0.5400 0.7069 -0.76 0.456
S = 3.99907 PRESS = 1023.52
R-Sq = 25.68% R-Sq(预测) = 0.00% R-Sq(调整) = 0.00%
我们利用显著水平α=0.05来判断显著的因子,发现没有一项是显著的。
阶段 2:分析残差图(residual plots), 确认模型的适合性
分析因子设计
1) Ctrl+E
2) 点击 图形
3) 完成如下对话框
4) 点击 确定
输出如下:
从残差图上可以观察到4个不正常的数据点。用刷子刷一下,就可知道对应数据工作表中对应的数据行行号,其中有2个不正常的数据点,因为2个复制,所以在图上显示有4个不正常的数据点。
研究人员对实验过程作了调查,设备在实验的结束阶段发生了损坏,维修人员进行了修理,保证了最后部分的实验完成。
焊接测量是破坏性的,并且劳动强度大。经过几天的实验与分析数据,得出二个结论。
 由于产生奇异点是不知道的,不能重复产生奇异点的条件。
 重新进行完整的实验是不现实的。
基于以上情况,我们只能针对已有的数据进行分析。
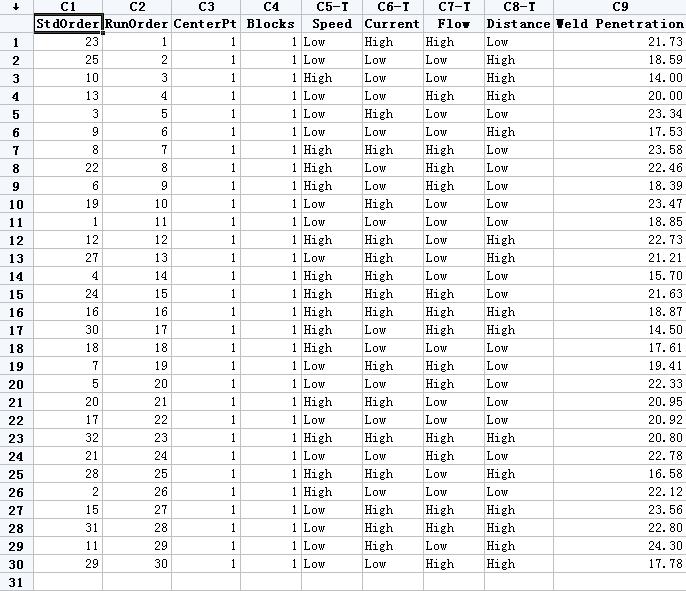
建立子集化工作表:
1) 选择 数据 > 子集化工作表
2) 完成下列对话框
3) 点击 确定
移去最后二行,再进行分析。
因移去了2行,原来的设计不再正交了,如果很多数据缺失(比如超过一半的数据),一些因子相关系数几乎达到1,意谓着他们的效应完全混杂(Confounded)了。
下面对正交性进行进一步的检查。
显示数据与相关性
1) 选择 统计 > DOE > 显示设计
2) 选择 已编码单位
3) 点击 确定
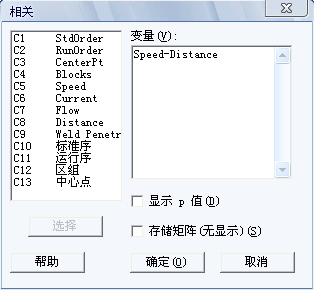
4) 选择 统计 > 基本统计 > 相关
5) 完成如下对话框
输出结果如下:
相关: Speed, Current, Flow, Distance
Speed Current Flow
Current 0.071
Flow 0.000 -0.000
Distance -0.071 0.071 0.000
从上面结果可以得出,正交性的失拟现象是很小的,所以我们可以选择减少模型来继续分析。事实上,我们几乎得到相同的模型,不管你用那种方法。
在MINITAB的DOE菜单中,不正交设计还是可以进行分析的,关键是我们已经了解了混杂的程度,并且在减少模型时,如有必要,每次减少一个因子。
显示设计与分析因子设计
1) 选择 统计 > DOE > 显示设计
2) 选择 未编码单位,然后点击 确定
3) 选择 统计 > DOE > 因子 > 分析因子设计
4) 在响应栏,输入 Weld Penetration(焊缝渗透深度)
5) 点击 图形,完成如下对话框
6) 点击 确定
输出如下:
拟合因子: Weld Penetration 与 Speed, Current, Flow, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 19.907 0.4131 48.19 0.000
Speed -2.511 -1.256 0.4131 -3.04 0.009
Current 2.769 1.384 0.4131 3.35 0.005
Flow 0.826 0.413 0.4131 1.00 0.334
Distance -2.095 -1.047 0.4131 -2.54 0.024
Speed*Current 0.139 0.069 0.4131 0.17 0.869
Speed*Flow 0.554 0.277 0.4131 0.67 0.514
Speed*Distance -1.213 -0.606 0.4131 -1.47 0.164
Current*Flow -0.314 -0.157 0.4131 -0.38 0.710
Current*Distance 2.225 1.113 0.4131 2.69 0.017
Flow*Distance -0.343 -0.171 0.4131 -0.41 0.685
SpeedCurrentFlow 1.164 0.582 0.4131 1.41 0.181
SpeedCurrentDistance 0.363 0.181 0.4131 0.44 0.667
SpeedFlowDistance -0.697 -0.349 0.4131 -0.84 0.413
CurrentFlowDistance 0.133 0.066 0.4131 0.16 0.875
SpeedCurrentFlow*Distance -1.142 -0.571 0.4131 -1.38 0.188
S = 2.20293 PRESS = *
R-Sq = 70.96% R-Sq(预测) = *% R-Sq(调整) = 39.85%
解释结果:
由于移去了2行数据缺失行,一些项已经是显著的了,Residual error S,SE Coef. 与原先相比,已经小了很多,说明一些奇异数据对实验的预估值影响是很大的 。
由于移去了2行数据缺失行,设计已不具备了正交性,要求你移去非显著的项时,先移去交互作用项,一次只能移去一项。但是,由于本设计很接近正交性,所以还是能够一次性地移走非显著项的,而并不影响最终模型的结果。
分析因子设计
1) Ctrl+E
2) 点击 项
3) 完成如下对话框
4) 点击 确定
5) 击点 图形
6) 选择四合一
7) 点击 确定
输出如下:
拟合因子: Weld Penetration 与 Speed, Current, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 19.985 0.3936 50.78 0.000
Speed -2.355 -1.178 0.3936 -2.99 0.006
Current 2.613 1.306 0.3936 3.32 0.003
Distance -1.939 -0.970 0.3936 -2.46 0.021
Current*Distance 2.069 1.035 0.3936 2.63 0.014
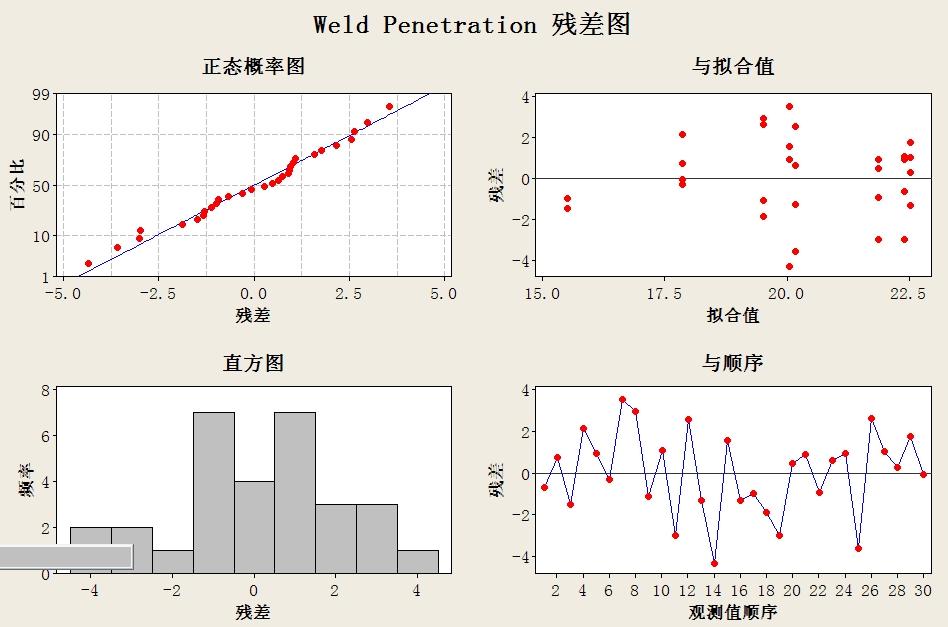
检查其残差图,没有显示不正常的特性。
最后的模型方程为:
在最后的模型中,Speed, Current, Distance 及 Current*Distance 是显著项,因而其方程为:
Weld Pen = 19.985 – 1.178Speed + 1.306Current
– 0.970Distance + 1.035Current*distance
 阶段3: 通过图表分析,分析主效应和交互作用效应
1) 选择 统计 > DOE > 因子 >因子图
2) 点击 主效应图
3) 点击 设置
4) 完成如下对话框
5) 点击 确定,完成对话框
6) 点击 交互作用图
7) 点击 设置
8) 完成如下对话框
9) 点击 确定,完成对话框
其主效应图如下:
从主效应图可以看出,随着速度(Speed)因子,从低水平到高水平的过程中,减少了焊缝渗透深度(Weld Penetration)2个单位的效应。
其交互作用图为:
从交互作用图可以看出,焊接电流(Current)与距离(Distance)有交互作用。在低水平的焊接电流(Current)下,距离(Distance)从低水平到高水平几乎减少了焊缝渗透深度(Weld Penetration)近4个单位的效应。
 阶段4 : 导出结论,提出方案。
通过实验,可以得出以下结论:
 增加火把/电极速度(Speed),将减少焊缝渗透深度,所以,要获得高的焊缝渗透深度,火把/电极速度(Speed)就必须设置在低水平。
 要获得大的焊缝渗透深度,焊接电流(Current)就必须设置高水平,基于以下二条理由:
- 高的焊接电流对形成焊缝渗透深度有利;
- 在实际生产过程中,高的焊接电流对焊缝渗透深度更加稳健。
 由于在焊接电流高水平时,距离的变化对响应的影响并不大,而且操作人员在研究的距离范围内调节比较容易实现。
 尽管气体流动速度(Flow)对响应有所影响,但影响并不大,不是显著因子。
得到的启发:
从模拟情况可以看出,我们设置的区域范围,工艺相对来说比较稳定,因子水平设置也比较容易。
 这个案例剖析了由于缺失数据的存在,造成了正交性与平衡性的失拟,导致了因子的效应不能独立预估,并降低了模型的精确度。如果稍有一些失拟,影响也比较小。但是,如果随着缺失数据的增加,失拟也在增大。
 数据缺失行,设计已不具备了正交性,要求你移去非显著的项时,先移去交互作用项,一次只能移去一项。这是一个逐步回归的过程,当然,通过功能强大的MINITAB的菜单能够轻易完成的。
 另一个技术,就是有效地处理这些缺失数据,然后再进行分析。要想详细了解另一种技术,请参见本人的《实验技术中奇异数据的处理技巧》一文。
1, Box, George E. P., William G. Hunter, and J. Stuart Hunter, Statistics for
Experimenters: An Introduction to Design, Data Analysis, and Model Building, New York, NY : John Wiley and Sons, Inc., 1978,
2, Box, George E.P., “Signal-to-Noise Ratios, Performance Criteria, and
Transformation.” Technometrics vol. 30, pp 1-40,1988
3, Cale, T.S., M.K. Jain, and G.B. Raupp, “Maximizing Step Coverage During Blanket
Tungsten Low Pressure Chemical Vapor Deposition, “Thin Solid Films vol. 193/194, pp. 51-60,1990
4, Applied Statistics and probability for engineers;Douglas C. Montgomery George C. Runger
5, Design and analysis of Experiments;Douglas C. Montgomery
The above 2 books are published by John Wiley & Sons,Inc.
6, 改进工艺,优化核心流程教材第五册,第六册,闵亚能 2005
7, Statistics for Experimenters. Wiley, New York. George E.P. Box, William G.Hunter, and J. Stuart Hunter(1978)
8, Statistical Design and Analysis of Experiments;Wiley, New York. Robert L. Mason, Richard F. Gunst, and James L. Hess(1989)
9, Design and Analysis of Experiments, 4th edition. Wiley, New York. Douglas C. Montgomery (1997)
10, Minitab Statistics and Graphics Guide, Minitab institute, State College, PA.
11, Minitab manual: Design of Experiment Guide & Statistics and Graphics Guide
12, Motorola University: Leadership, Learning & Performance serial books.
-- 利用缺失数据进行实验设计的成功一例
上海先进半导体制造股份有限公司 6Sigma经理 高级工程师 闵亚能
内 容 提 要
通过获得最佳的焊缝渗透的工艺参数的实验设计,剖析了由于缺失数据的存在,造成了正交性与平衡性的失拟,导致了因子的效应不能独立预估,并降低了模型的精确度。通过对失拟的程度评判作出决策,如果稍有一些失拟,影响也比较小,但是,如果随着缺失数据的增加,失拟也在增大。针对多数情况,还是可以通过功能强大的MINITAB的菜单操作能够轻易完成的。本实验的成功应用到实际工作中,开创了解决异常问题的复杂实验设计的新局面。
实验设计 缺失数据分析 实验精确度
概述
什么是实验设计中的缺失数据?
如果一个或多个实验处理没有响应值,那么DOE的分析涉及到缺失数据的分析。
什么时候在设计的实验中会发生缺失数据?
有好几种情况导致不完全的实验设计的发生,形成了实验中的缺失数据:
 实验被停止,因为完成实验所需要的资源不再提供,如没有时间、资金、原材料等。
 从实验中获得的数据不正确的,在残差分析中出现明显的奇异数据。观察到的奇异数据,常常是由于测量错误,数据登录错误,不寻常的环境条件,和实验设置的问题。
 观察到的数据丢失了。
在实验设计中怎样分析缺失数据?
你可以使用 MINITAB 的DOE 菜单来分析,虽然设计一般不再正交,但是,我们通过评估缺失数据对模型的影响程度,利用逐步回归进行分析,在减少模型时,一次减少一个因子的方法,最后得到简化的适合模型。
问题的由来
一种钨(惰性气体)焊接操作是在二块钢板之间产生一条焊缝,焊缝渗透深度会影响装配件的使用寿命。期望获得较大的焊缝渗透深度,制造厂购买了一种新的焊接设备。 工程师进行试验来找出以获得最佳的焊缝渗透深度的工艺设计参数。
焊接工艺关键的可控制的变量是:
火把/电极速度(Speed),焊接电流(Current),气体流动速度(Flow)和工件到焊接点的距离(Distance)。这些因子有些在实际应用中有交互作用,因此工程师们创建了一个全因子设计来考虑和估计交互作用。他们复制了一个全因子实验设计,以获得更好的因子主效应与交互作用的效应估计。
数据收集
数据文件Missingdata.MPJ
变量 描述
StdOrder 标准序
RunOrder 运行序
CenterPt 中心点
Block 区组
速度(Speed) 电极速度
焊接电流(Current) 焊接电流
流速(Flow) 气体流速
距离(Distance) 工件和电极尖端的距离
焊缝渗透深度(Weld Penetration) 二块钢板的焊缝深度
分析步骤
 阶段 1 : 制定完全模型(Full model)的 ANOVA表,解释结果
1) 打开文件 MISSINGDATA.MPJ
2) 选择 统计 > DOE > 因子 > 分析因子设计
3) 在响应栏选择 Weld Penetration(焊缝渗透深度)
4) 点击 项
5) 完成如下对话框
6) 点击 确定
结果分析
拟合因子: Weld Penetration 与 Speed, Current, Flow, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 20.7631 0.7069 29.37 0.000
Speed -0.7988 -0.3994 0.7069 -0.56 0.580
Current 1.0563 0.5281 0.7069 0.75 0.466
Flow 0.7637 0.3819 0.7069 0.54 0.597
Distance -0.3825 -0.1912 0.7069 -0.27 0.790
Speed*Current -1.5738 -0.7869 0.7069 -1.11 0.282
Speed*Flow 0.4912 0.2456 0.7069 0.35 0.733
Speed*Distance 0.5000 0.2500 0.7069 0.35 0.728
Current*Flow -0.2512 -0.1256 0.7069 -0.18 0.861
Current*Distance 0.5125 0.2563 0.7069 0.36 0.722
Flow*Distance -0.4050 -0.2025 0.7069 -0.29 0.778
SpeedCurrentFlow 1.2263 0.6131 0.7069 0.87 0.399
SpeedCurrentDistance -1.3500 -0.6750 0.7069 -0.95 0.354
SpeedFlowDistance -0.7600 -0.3800 0.7069 -0.54 0.598
CurrentFlowDistance 0.1950 0.0975 0.7069 0.14 0.892
SpeedCurrentFlow*Distance -1.0800 -0.5400 0.7069 -0.76 0.456
S = 3.99907 PRESS = 1023.52
R-Sq = 25.68% R-Sq(预测) = 0.00% R-Sq(调整) = 0.00%
我们利用显著水平α=0.05来判断显著的因子,发现没有一项是显著的。
阶段 2:分析残差图(residual plots), 确认模型的适合性
分析因子设计
1) Ctrl+E
2) 点击 图形
3) 完成如下对话框
4) 点击 确定
输出如下:
从残差图上可以观察到4个不正常的数据点。用刷子刷一下,就可知道对应数据工作表中对应的数据行行号,其中有2个不正常的数据点,因为2个复制,所以在图上显示有4个不正常的数据点。
研究人员对实验过程作了调查,设备在实验的结束阶段发生了损坏,维修人员进行了修理,保证了最后部分的实验完成。
焊接测量是破坏性的,并且劳动强度大。经过几天的实验与分析数据,得出二个结论。
 由于产生奇异点是不知道的,不能重复产生奇异点的条件。
 重新进行完整的实验是不现实的。
基于以上情况,我们只能针对已有的数据进行分析。
建立子集化工作表:
1) 选择 数据 > 子集化工作表
2) 完成下列对话框
3) 点击 确定
移去最后二行,再进行分析。
因移去了2行,原来的设计不再正交了,如果很多数据缺失(比如超过一半的数据),一些因子相关系数几乎达到1,意谓着他们的效应完全混杂(Confounded)了。
下面对正交性进行进一步的检查。
显示数据与相关性
1) 选择 统计 > DOE > 显示设计
2) 选择 已编码单位
3) 点击 确定
4) 选择 统计 > 基本统计 > 相关
5) 完成如下对话框
输出结果如下:
相关: Speed, Current, Flow, Distance
Speed Current Flow
Current 0.071
Flow 0.000 -0.000
Distance -0.071 0.071 0.000
从上面结果可以得出,正交性的失拟现象是很小的,所以我们可以选择减少模型来继续分析。事实上,我们几乎得到相同的模型,不管你用那种方法。
在MINITAB的DOE菜单中,不正交设计还是可以进行分析的,关键是我们已经了解了混杂的程度,并且在减少模型时,如有必要,每次减少一个因子。
显示设计与分析因子设计
1) 选择 统计 > DOE > 显示设计
2) 选择 未编码单位,然后点击 确定
3) 选择 统计 > DOE > 因子 > 分析因子设计
4) 在响应栏,输入 Weld Penetration(焊缝渗透深度)
5) 点击 图形,完成如下对话框
6) 点击 确定
输出如下:
拟合因子: Weld Penetration 与 Speed, Current, Flow, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 19.907 0.4131 48.19 0.000
Speed -2.511 -1.256 0.4131 -3.04 0.009
Current 2.769 1.384 0.4131 3.35 0.005
Flow 0.826 0.413 0.4131 1.00 0.334
Distance -2.095 -1.047 0.4131 -2.54 0.024
Speed*Current 0.139 0.069 0.4131 0.17 0.869
Speed*Flow 0.554 0.277 0.4131 0.67 0.514
Speed*Distance -1.213 -0.606 0.4131 -1.47 0.164
Current*Flow -0.314 -0.157 0.4131 -0.38 0.710
Current*Distance 2.225 1.113 0.4131 2.69 0.017
Flow*Distance -0.343 -0.171 0.4131 -0.41 0.685
SpeedCurrentFlow 1.164 0.582 0.4131 1.41 0.181
SpeedCurrentDistance 0.363 0.181 0.4131 0.44 0.667
SpeedFlowDistance -0.697 -0.349 0.4131 -0.84 0.413
CurrentFlowDistance 0.133 0.066 0.4131 0.16 0.875
SpeedCurrentFlow*Distance -1.142 -0.571 0.4131 -1.38 0.188
S = 2.20293 PRESS = *
R-Sq = 70.96% R-Sq(预测) = *% R-Sq(调整) = 39.85%
解释结果:
由于移去了2行数据缺失行,一些项已经是显著的了,Residual error S,SE Coef. 与原先相比,已经小了很多,说明一些奇异数据对实验的预估值影响是很大的 。
由于移去了2行数据缺失行,设计已不具备了正交性,要求你移去非显著的项时,先移去交互作用项,一次只能移去一项。但是,由于本设计很接近正交性,所以还是能够一次性地移走非显著项的,而并不影响最终模型的结果。
分析因子设计
1) Ctrl+E
2) 点击 项
3) 完成如下对话框
4) 点击 确定
5) 击点 图形
6) 选择四合一
7) 点击 确定
输出如下:
拟合因子: Weld Penetration 与 Speed, Current, Distance
Weld Penetration 的效应和系数的估计(已编码单位)
项 效应 系数 系数标准误 T P
常量 19.985 0.3936 50.78 0.000
Speed -2.355 -1.178 0.3936 -2.99 0.006
Current 2.613 1.306 0.3936 3.32 0.003
Distance -1.939 -0.970 0.3936 -2.46 0.021
Current*Distance 2.069 1.035 0.3936 2.63 0.014
检查其残差图,没有显示不正常的特性。
最后的模型方程为:
在最后的模型中,Speed, Current, Distance 及 Current*Distance 是显著项,因而其方程为:
Weld Pen = 19.985 – 1.178Speed + 1.306Current
– 0.970Distance + 1.035Current*distance
 阶段3: 通过图表分析,分析主效应和交互作用效应
1) 选择 统计 > DOE > 因子 >因子图
2) 点击 主效应图
3) 点击 设置
4) 完成如下对话框
5) 点击 确定,完成对话框
6) 点击 交互作用图
7) 点击 设置
8) 完成如下对话框
9) 点击 确定,完成对话框
其主效应图如下:
从主效应图可以看出,随着速度(Speed)因子,从低水平到高水平的过程中,减少了焊缝渗透深度(Weld Penetration)2个单位的效应。
其交互作用图为:
从交互作用图可以看出,焊接电流(Current)与距离(Distance)有交互作用。在低水平的焊接电流(Current)下,距离(Distance)从低水平到高水平几乎减少了焊缝渗透深度(Weld Penetration)近4个单位的效应。
 阶段4 : 导出结论,提出方案。
通过实验,可以得出以下结论:
 增加火把/电极速度(Speed),将减少焊缝渗透深度,所以,要获得高的焊缝渗透深度,火把/电极速度(Speed)就必须设置在低水平。
 要获得大的焊缝渗透深度,焊接电流(Current)就必须设置高水平,基于以下二条理由:
- 高的焊接电流对形成焊缝渗透深度有利;
- 在实际生产过程中,高的焊接电流对焊缝渗透深度更加稳健。
 由于在焊接电流高水平时,距离的变化对响应的影响并不大,而且操作人员在研究的距离范围内调节比较容易实现。
 尽管气体流动速度(Flow)对响应有所影响,但影响并不大,不是显著因子。
得到的启发:
从模拟情况可以看出,我们设置的区域范围,工艺相对来说比较稳定,因子水平设置也比较容易。
 这个案例剖析了由于缺失数据的存在,造成了正交性与平衡性的失拟,导致了因子的效应不能独立预估,并降低了模型的精确度。如果稍有一些失拟,影响也比较小。但是,如果随着缺失数据的增加,失拟也在增大。
 数据缺失行,设计已不具备了正交性,要求你移去非显著的项时,先移去交互作用项,一次只能移去一项。这是一个逐步回归的过程,当然,通过功能强大的MINITAB的菜单能够轻易完成的。
 另一个技术,就是有效地处理这些缺失数据,然后再进行分析。要想详细了解另一种技术,请参见本人的《实验技术中奇异数据的处理技巧》一文。
1, Box, George E. P., William G. Hunter, and J. Stuart Hunter, Statistics for
Experimenters: An Introduction to Design, Data Analysis, and Model Building, New York, NY : John Wiley and Sons, Inc., 1978,
2, Box, George E.P., “Signal-to-Noise Ratios, Performance Criteria, and
Transformation.” Technometrics vol. 30, pp 1-40,1988
3, Cale, T.S., M.K. Jain, and G.B. Raupp, “Maximizing Step Coverage During Blanket
Tungsten Low Pressure Chemical Vapor Deposition, “Thin Solid Films vol. 193/194, pp. 51-60,1990
4, Applied Statistics and probability for engineers;Douglas C. Montgomery George C. Runger
5, Design and analysis of Experiments;Douglas C. Montgomery
The above 2 books are published by John Wiley & Sons,Inc.
6, 改进工艺,优化核心流程教材第五册,第六册,闵亚能 2005
7, Statistics for Experimenters. Wiley, New York. George E.P. Box, William G.Hunter, and J. Stuart Hunter(1978)
8, Statistical Design and Analysis of Experiments;Wiley, New York. Robert L. Mason, Richard F. Gunst, and James L. Hess(1989)
9, Design and Analysis of Experiments, 4th edition. Wiley, New York. Douglas C. Montgomery (1997)
10, Minitab Statistics and Graphics Guide, Minitab institute, State College, PA.
11, Minitab manual: Design of Experiment Guide & Statistics and Graphics Guide
12, Motorola University: Leadership, Learning & Performance serial books.
没有找到相关结果
已邀请:















3 个回复
ichiroliu (威望:2) (台湾 台北县) 电子制造 主管 - 詩詞歌賦
赞同来自:
恕我冒昧提出疑問...
看到下列的數字, 發現這個model的解釋能力似乎很低...R-Sq (adj)=39.85%
S = 2.20293 PRESS = *
R-Sq = 70.96% R-Sq(预测) = *% R-Sq(调整) = 39.85%